题目内容
13.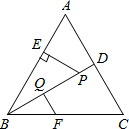 如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,求PE的长.
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,求PE的长.
分析 在直角△BFQ中,利用三角函数即可求得BQ的长,则BP的长即可求得,然后在直角△BPE中,利用30度所对的直角边等于斜边的一半即可求得PE的长.
解答 解:∵△ABC是等边三角形.P是∠ABC的平分线BD上一点,
∴∠FBQ=∠EBP=30°,
∴在直角△BFQ中,BQ=BF•cos∠FBQ=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
又∵QF是BP的垂直平分线,
∴BP=2BQ=2$\sqrt{3}$.
∵直角△BPE中,∠EBP=30°,
∴PE=$\frac{1}{2}$BP=$\sqrt{3}$.
点评 本题考查了等边三角形的性质以及直角三角形的性质和三角函数,正确求得BQ的长是关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
4.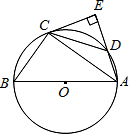 如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=10,AC=8,求tan∠DCE的值.
 如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.(1)求证:DC=BC;
(2)若AB=10,AC=8,求tan∠DCE的值.
1.下列各图中,能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
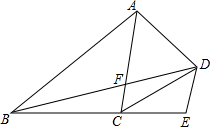 四边形ABCD中,AD=CD,∠ADB=∠ACB,DE∥AC,交BC延于E,求证:AD2=AF•DE.
四边形ABCD中,AD=CD,∠ADB=∠ACB,DE∥AC,交BC延于E,求证:AD2=AF•DE.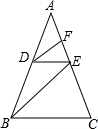 已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.
已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.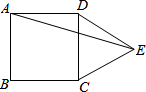 如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.
如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.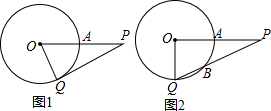 已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.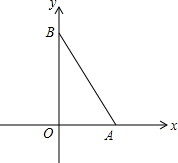 已知点A的坐标为(2,0),点B的坐标为(0,4),作等边△ABC,求点C的坐标.
已知点A的坐标为(2,0),点B的坐标为(0,4),作等边△ABC,求点C的坐标.