题目内容
求下列三角形的外接圆半径R和内切圆半径r.
(1)等边△ABC,边长为6;
(2)在△ABC中,AB=AC=13,BC=24;
(3)Rt△ABC,∠C=90°,AC=5,BC=12.
(1)等边△ABC,边长为6;
(2)在△ABC中,AB=AC=13,BC=24;
(3)Rt△ABC,∠C=90°,AC=5,BC=12.
考点:三角形的外接圆与外心,三角形的内切圆与内心
专题:
分析:(1)过圆心作一边的垂线,解直角三角形即可求出外接圆半径和内切圆;
(2)根据等腰三角形的性质得出内心和外心都在底边的高AD上,根据勾股定理得出方程,即可求出外接圆的半径,根据三角形的面积公式即可求出内切圆的半径;
(3)根据勾股定理求出斜边,即可得出外接圆的半径画出图形,根据切线长定理求出BF=BD,AF=AE,求出四边形DCEO是正方形,得出OD=OE=DC=CE,得出方程,求出即可.
(2)根据等腰三角形的性质得出内心和外心都在底边的高AD上,根据勾股定理得出方程,即可求出外接圆的半径,根据三角形的面积公式即可求出内切圆的半径;
(3)根据勾股定理求出斜边,即可得出外接圆的半径画出图形,根据切线长定理求出BF=BD,AF=AE,求出四边形DCEO是正方形,得出OD=OE=DC=CE,得出方程,求出即可.
解答:解:(1)如图1,

△ABC是正三角形,设O是△ABC的中心(也是等边三角形ABC的内心),
则∠OBD=30°,
∵正三角形的边长为6,
∴BD=
BC=
×6=3,OD=BD•tan30°=3×
=
,
OB=2OD=2
,
即三角形的外接圆半径R=2
,内切圆半径r=
;
(2)如图2,

∵在△ABC中,AB=AC=13,BC=24,
∴过A作AD⊥BC于D,则外接圆的圆心O在AD上,连接OB、OC,
∴BD=CD=
BC=12,AD=
=5,
∵在Rt△OBD中,由勾股定理得:OB2=OD2+BD2,
∴R2=(5-R)2+122,
∴R=16.9;
如图3,

故A作AD⊥BC于D,
∵△ABC中,AB=AC,
∴△ABC的外心I在AD上,过I作IE⊥AC于E,IF⊥AB于F,连接OA、OB、OC,
则IF=IE=ID=r,
∵S△ABC=S△BIC+S△AIC+S△ABI,
∴由三角形的面积公式得:
BC×AD=
BC×r+
AC×r+
AB×r,
∴12×5=12r+13r+13r,
∴r=
,
即三角形ABC的外接圆半径R=16.9,内切圆半径r=
;
(3)如图4,

接圆的圆心是斜边AB的中点,
由勾股定理得:AB
=
=13,
所以外接圆的半径为
AB=6.5,
连接OD、OE,如图5,

∵⊙O是△ACB的内切圆,
∴BD=BF,AE=AF,CD=CE,∠ODC=∠C=∠OEC=90°,
∵OD=OE,
∴四边形DCEO是正方形,
∴OD=DC=OE=CE,
∵AB=13,
∴BF+AF=BD+AE=12-OD+5-OE=13,
∴OD=OE=2,
即三角形ABC的外接圆半径R=6.5,内切圆半径r=2.

△ABC是正三角形,设O是△ABC的中心(也是等边三角形ABC的内心),
则∠OBD=30°,
∵正三角形的边长为6,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 3 |
OB=2OD=2
| 3 |
即三角形的外接圆半径R=2
| 3 |
| 3 |
(2)如图2,

∵在△ABC中,AB=AC=13,BC=24,
∴过A作AD⊥BC于D,则外接圆的圆心O在AD上,连接OB、OC,
∴BD=CD=
| 1 |
| 2 |
| 132-122 |
∵在Rt△OBD中,由勾股定理得:OB2=OD2+BD2,
∴R2=(5-R)2+122,
∴R=16.9;
如图3,

故A作AD⊥BC于D,
∵△ABC中,AB=AC,
∴△ABC的外心I在AD上,过I作IE⊥AC于E,IF⊥AB于F,连接OA、OB、OC,
则IF=IE=ID=r,
∵S△ABC=S△BIC+S△AIC+S△ABI,
∴由三角形的面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴12×5=12r+13r+13r,
∴r=
| 30 |
| 19 |
即三角形ABC的外接圆半径R=16.9,内切圆半径r=
| 30 |
| 19 |
(3)如图4,

接圆的圆心是斜边AB的中点,
由勾股定理得:AB
| AC2+BC2 |
| 52+122 |
所以外接圆的半径为
| 1 |
| 2 |
连接OD、OE,如图5,

∵⊙O是△ACB的内切圆,
∴BD=BF,AE=AF,CD=CE,∠ODC=∠C=∠OEC=90°,
∵OD=OE,
∴四边形DCEO是正方形,
∴OD=DC=OE=CE,
∵AB=13,
∴BF+AF=BD+AE=12-OD+5-OE=13,
∴OD=OE=2,
即三角形ABC的外接圆半径R=6.5,内切圆半径r=2.
点评:本题考查了三角形的外接圆和内切圆,勾股定理,三角形的面积,解直角三角形的应用,能综合运用性质进行推理和计算是解此题的关键,有一定的难度.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
若(x-4)0-(2x-6)-2有意义,则x的取值范围是( )
| A、x>4 |
| B、x<3 |
| C、x≠4或x≠3 |
| D、x≠4且x≠3 |


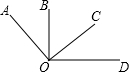 如图,∠AOC=∠BOD=90°,且∠DOC:∠BOC=2:7,求∠AOB,∠AOD的度数.
如图,∠AOC=∠BOD=90°,且∠DOC:∠BOC=2:7,求∠AOB,∠AOD的度数. 如图,△ABC绕点A旋转后能与△ADE重合,
如图,△ABC绕点A旋转后能与△ADE重合,