题目内容
在2013年3月12日植树节,由兰华社区联合组织开展了第二届网友植树造林活动,在这次活动中,种植了杨树和杉树两类树种,已知种植杨树的棵数比总数的一半多56棵,种植杉树的棵树比总数的
少14棵,这两类树各种植了多少棵?
| 1 |
| 3 |
考点:二元一次方程组的应用
专题:
分析:设杨树种植了x棵,杉树种植了y棵,根据树的棵数比总数的一半多56棵可以得出方程x=
+56,由植杉树的棵树比总数的
少14棵可以得出方程y=
-14,由这两个方程构成方程组,求出其解即可.
| x+y |
| 2 |
| 1 |
| 3 |
| x+y |
| 3 |
解答:解:设杨树有x棵,杉树有y棵,由题意,得
,
解得:
.
答:杨树种植了182棵,杉树种植了70棵.
|
解得:
|
答:杨树种植了182棵,杉树种植了70棵.
点评:本题考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,解答时根据条件建立二元一次方程组是关键.

练习册系列答案
相关题目
已知α为锐角,且cosα≤sin30°,则( )
| A、0°≤α≤60° |
| B、60°≤α<90° |
| C、0°<α≤30° |
| D、30°≤α<90° |
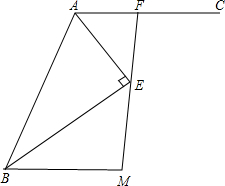 如图,AE平分∠BAC,BE⊥AE,AC∥BM,若AB=5,BM=4,求AF的长.
如图,AE平分∠BAC,BE⊥AE,AC∥BM,若AB=5,BM=4,求AF的长.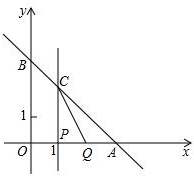 已知直线y=-x+3分别交x轴,y轴于A,B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,线段OA上另有一动点Q由点A向点O运动,它与点P以同样速度同时出发,当点P到达点A时两点同时停止运动(如图),设运动时间为t秒.
已知直线y=-x+3分别交x轴,y轴于A,B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,线段OA上另有一动点Q由点A向点O运动,它与点P以同样速度同时出发,当点P到达点A时两点同时停止运动(如图),设运动时间为t秒.