题目内容
已知x2-
x+1=0,求:
(1)x2+
;
(2)x-
的值.
| 10 |
(1)x2+
| 1 |
| x2 |
(2)x-
| 1 |
| x |
考点:分式的混合运算,完全平方公式
专题:
分析:由x2-
x+1=0,两边同除以x得出x+
=
;
(1)把原式变为(x+
)2-2,代入求得数值即可;
(2)把x-
平方,再把(1)的结果代入求得数值,进一步开方得出答案即可.
| 10 |
| 1 |
| x |
| 10 |
(1)把原式变为(x+
| 1 |
| x |
(2)把x-
| 1 |
| x |
解答:解:∵x2-
x+1=0,
∴x+
=
;
(1)x2+
=(x+
)2-2
=10-2
=8;
(2)∵(x-
)2=x2+
-2=8-2=6,
∴x-
=
.
| 10 |
∴x+
| 1 |
| x |
| 10 |
(1)x2+
| 1 |
| x2 |
=(x+
| 1 |
| x |
=10-2
=8;
(2)∵(x-
| 1 |
| x |
| 1 |
| x2 |
∴x-
| 1 |
| x |
| 6 |
点评:此题考查分式的混合运算,注意利用式子的特点,利用完全平方公式巧妙变形,利用整体代入的思想解决问题.

练习册系列答案
相关题目
 如图,在标号的11个角中同位角有
如图,在标号的11个角中同位角有 如图,已知∠AOB和点P.
如图,已知∠AOB和点P.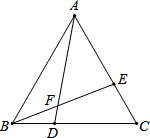 如图,△ABC中,AB=AC,D、E分别是BC、AC上的点,AD与BE交于点F.试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题.
如图,△ABC中,AB=AC,D、E分别是BC、AC上的点,AD与BE交于点F.试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题.