题目内容
已知α为锐角,且cosα≤sin30°,则( )
| A、0°≤α≤60° |
| B、60°≤α<90° |
| C、0°<α≤30° |
| D、30°≤α<90° |
考点:锐角三角函数的增减性
专题:
分析:根据一个角的余弦等于它余角的正弦,可得60°角的余弦,根据锐角的余弦函数随角的增大而减小,可得答案.
解答:解:由一个角的正弦等于它余角的余弦,得
cosα≤sin30°=cos60°=
,
由锐角余弦函数随角的增大而减小,得
60≤α≤90°,
cosα≤sin30°=cos60°=
| 1 |
| 2 |
由锐角余弦函数随角的增大而减小,得
60≤α≤90°,
点评:本题考查了锐角三角函数的增减性,利用一个角的余弦等于它余角的正弦,锐角的余弦函数随角的增大而减小

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,⊙O上有A,B,C,D四点,其中∠A=80°,那么∠C的度数是( )
如图,⊙O上有A,B,C,D四点,其中∠A=80°,那么∠C的度数是( )| A、40° | B、60° |
| C、80° | D、100° |
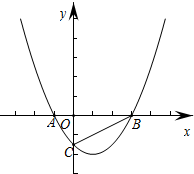 如图,抛物线y=
如图,抛物线y= 如图,在标号的11个角中同位角有
如图,在标号的11个角中同位角有