题目内容
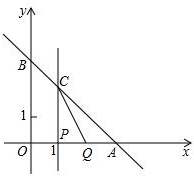 已知直线y=-x+3分别交x轴,y轴于A,B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,线段OA上另有一动点Q由点A向点O运动,它与点P以同样速度同时出发,当点P到达点A时两点同时停止运动(如图),设运动时间为t秒.
已知直线y=-x+3分别交x轴,y轴于A,B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,线段OA上另有一动点Q由点A向点O运动,它与点P以同样速度同时出发,当点P到达点A时两点同时停止运动(如图),设运动时间为t秒.(1)直接写出点A,B的坐标;
(2)求tan∠QCP的值(用含t的代数式表示);
(3)若以Q,C,A为顶点的三角形与△AOB相似,求t的值.
考点:一次函数综合题,相似三角形的判定与性质,锐角三角函数的定义
专题:综合题,分类讨论
分析:(1)根据坐标轴上点的坐标特征,就可求出点A、点B的坐标;
(2)可分三种情况(①点P在点Q的左边,②点P与点Q重合,③点P在点Q的右边)讨论,然后只需用t的代数式表示出CP、PQ,就可解决问题;
(3)两个相似三角形对应关系不确定,故需分两种情况(①△ACQ∽△ABO,②△ACQ∽△AOB)讨论,然后只需运用相似三角形的性质就可求出t的值.
(2)可分三种情况(①点P在点Q的左边,②点P与点Q重合,③点P在点Q的右边)讨论,然后只需用t的代数式表示出CP、PQ,就可解决问题;
(3)两个相似三角形对应关系不确定,故需分两种情况(①△ACQ∽△ABO,②△ACQ∽△AOB)讨论,然后只需运用相似三角形的性质就可求出t的值.
解答:解:(1)∵直线y=-x+3分别交x轴,y轴于A,B两点,
∴点A的坐标为(3,0),点B的坐标为(0,3).
(2)∵A(3,0),B(0,3),
∴OA=OB=3.
∵∠AOB=90°,∴∠OAB=45°.
∵CP⊥OA,即∠CPA=90,
∴∠PCA=∠PAC=45°,
∴PC=PA.
由题可得:OP=AQ=1×t=t,
∴PC=PA=OA-OP=3-x.
①当点P在点Q的左边时,0<t<
,
此时PQ=OA-OP-AQ=3-2t.
在Rt△CPQ中,tan∠QCP=
=
;
②当点P与点Q重合时,t=
,
tan∠QCP=tan0°=0;
③当点P在点Q的右边时,
<t<3,
此时PQ=AQ-AP=AQ-(OA-OP)=t-(3-t)=2t-3.
在Rt△CPQ中,tan∠QCP=
=
.
(3)在Rt△AOB中,
AB=
=
=3
.
在Rt△CPA中,
AC=
=
=
(3-t).
①若△ACQ∽△ABO,
则
=
,
∴
=
,
解得:t=
;
②若△ACQ∽△AOB,
则
=
,
∴
=
,
解得:t=2.
综上所述:t的值为
或2.
∴点A的坐标为(3,0),点B的坐标为(0,3).
(2)∵A(3,0),B(0,3),
∴OA=OB=3.
∵∠AOB=90°,∴∠OAB=45°.
∵CP⊥OA,即∠CPA=90,
∴∠PCA=∠PAC=45°,

∴PC=PA.
由题可得:OP=AQ=1×t=t,
∴PC=PA=OA-OP=3-x.
①当点P在点Q的左边时,0<t<
| 3 |
| 2 |
此时PQ=OA-OP-AQ=3-2t.
在Rt△CPQ中,tan∠QCP=
| PQ |
| CP |
| 3-2t |
| 3-x |
②当点P与点Q重合时,t=
| 3 |
| 2 |
tan∠QCP=tan0°=0;
③当点P在点Q的右边时,
| 3 |
| 2 |
此时PQ=AQ-AP=AQ-(OA-OP)=t-(3-t)=2t-3.
在Rt△CPQ中,tan∠QCP=
| PQ |
| CP |
| 2t-3 |
| 3-x |
(3)在Rt△AOB中,
AB=
| OA2+OB2 |
| 32+32 |
| 2 |
在Rt△CPA中,
AC=
| AP2+CP2 |
| (3-t)2+(3-t)2 |
| 2 |
①若△ACQ∽△ABO,
则
| AC |
| AB |
| AQ |
| AO |
∴
| ||
3
|
| t |
| 3 |
解得:t=
| 3 |
| 2 |
②若△ACQ∽△AOB,
则
| AC |
| AO |
| AQ |
| AB |
∴
| ||
| 3 |
| t | ||
3
|
解得:t=2.
综上所述:t的值为
| 3 |
| 2 |
点评:本题主要考查了坐标轴上点的坐标特征、等腰三角形的判定与性质、三角函数、勾股定理、相似三角形的判定与性质等知识,运用分类讨论的思想是解决本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,⊙O上有A,B,C,D四点,其中∠A=80°,那么∠C的度数是( )
如图,⊙O上有A,B,C,D四点,其中∠A=80°,那么∠C的度数是( )| A、40° | B、60° |
| C、80° | D、100° |
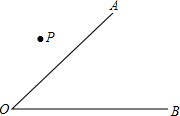 如图,已知∠AOB和点P.
如图,已知∠AOB和点P. 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE. 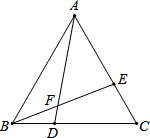 如图,△ABC中,AB=AC,D、E分别是BC、AC上的点,AD与BE交于点F.试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题.
如图,△ABC中,AB=AC,D、E分别是BC、AC上的点,AD与BE交于点F.试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题.