题目内容
16．
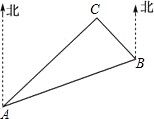如图，C岛在A岛的北偏东50°方向，C岛在B岛的北偏西40°方向，则从C岛看A，B两岛的视角∠ACB等于（ ）| A． | 90° | B． | 80° | C． | 70° | D． | 60° |
分析 根据平行线的性质，可得答案．
解答 解：如图：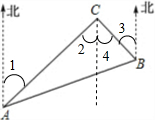
，
∠2=∠1=50°，∠4=∠3=40°，
∠ACB=∠2+∠4=90°．
故选：A．
点评 本题考查了方向角，利用数形结合是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．化简$\frac{x-y}{\sqrt{x}+\sqrt{y}}$，甲、乙两位同学的解法如下：
甲：$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{（x-y）（\sqrt{x}-\sqrt{y}）}{（\sqrt{x}+\sqrt{y}）（\sqrt{x}-\sqrt{y}）}$=$\sqrt{x}$-$\sqrt{y}$；
乙：$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{（\sqrt{x}+\sqrt{y}）（\sqrt{x}-\sqrt{y}）}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$．
对于甲、乙两位同学的解法，正确的判断是（ ）
甲：$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{（x-y）（\sqrt{x}-\sqrt{y}）}{（\sqrt{x}+\sqrt{y}）（\sqrt{x}-\sqrt{y}）}$=$\sqrt{x}$-$\sqrt{y}$；
乙：$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{（\sqrt{x}+\sqrt{y}）（\sqrt{x}-\sqrt{y}）}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$．
对于甲、乙两位同学的解法，正确的判断是（ ）
| A． | 甲、乙都正确 | B． | 甲正确，乙不正确 | C． | 甲、乙都不正确 | D． | 乙正确，甲不正确 |
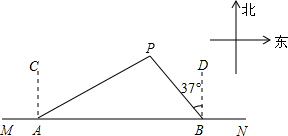如图，船A、B在东西方向的海岸线MN上，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东62°方向上，在船B的北偏西37°方向上，若AP=30海里．求船B到船P的距离PB（结果用含非特殊角的三角函数表示即可）．