题目内容
9.化简$\frac{x-y}{\sqrt{x}+\sqrt{y}}$,甲、乙两位同学的解法如下:甲:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$=$\sqrt{x}$-$\sqrt{y}$;
乙:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$.
对于甲、乙两位同学的解法,正确的判断是( )
| A. | 甲、乙都正确 | B. | 甲正确,乙不正确 | C. | 甲、乙都不正确 | D. | 乙正确,甲不正确 |
分析 根据平方差公式,可分母有理化.
解答 解:甲:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$=$\sqrt{x}$-$\sqrt{y}$;
乙:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$,
故选:A.
点评 本题考查了分母有理化,利用平方差公式是分母有理化的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
14.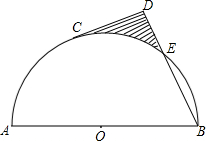 如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
 如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )| A. | 8$\sqrt{3}$-4π | B. | 8$\sqrt{3}$-$\frac{8}{3}$π | C. | 4π-6$\sqrt{3}$ | D. | 6$\sqrt{3}$-$\frac{8}{3}$π |
16.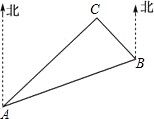 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )| A. | 90° | B. | 80° | C. | 70° | D. | 60° |
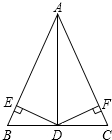 如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.
如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.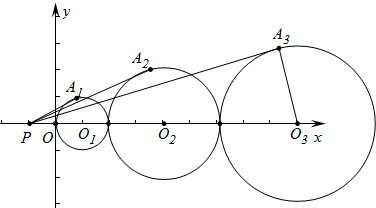 如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.
如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.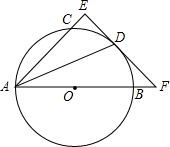 如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.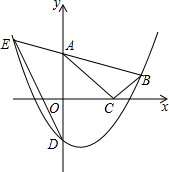 如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.