题目内容
4.已知一个两位数$\overline{pq}$,(p为十位数,q为个位数)使得二次函数y=x2+qx+p的图象与x轴交于不同的两点A、B,顶点为C,且S△ABC=$\overline{1}$,则符合条件的两位数pq为34,86.分析 令抛物线y=0,运用两点间的距离和根与系数的关系求出AB长度,运用顶点公式求出三角形的高,根据题意列方程求解即可.
解答 解:二次函数y=x2+qx+p,当y=0时,
x2+qx+p=0,设方程的两个根为:x1,x2,
则有AB=|x1-x2|=$\sqrt{{q}^{2}-4p}$,
y=x2+qx+p的顶点为:($-\frac{q}{2}$,$\frac{4p-{q}^{2}}{4}$),
此时,△ABC的高为:-$\frac{4p-{q}^{2}}{4}$,
∵S△ABC=1,
∴$\frac{1}{2}$×$\sqrt{{q}^{2}-4p}$×(-$\frac{4p-{q}^{2}}{4}$)=1,
解得:q2-4p=4,
此时q=2$\sqrt{p+1}$,
∵p,q为非负整数,且p≠0,
∴p=3,或p=8,
此时q=4,或q=6,
∴符合条件的两位数pq为:34或86;
故答案为:34,86.
点评 此题主要考查抛物线与坐标轴的交点问题,会结合方程的根求抛物线与x轴的交点的距离,会求抛物线顶点,会根据等式进行合理性分析是解题的关键.

练习册系列答案
相关题目
16.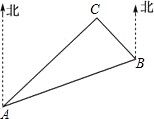 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )| A. | 90° | B. | 80° | C. | 70° | D. | 60° |
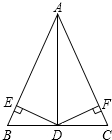 如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.
如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.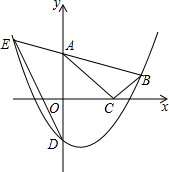 如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.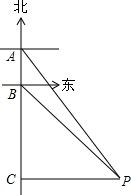 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)