题目内容
1.解不等式组$\left\{\begin{array}{l}{2(m+1.5)≥5}\\{\frac{5}{2}m<m+3}\end{array}\right.$.分析 先求出不等式组中每一个不等式的解集,再求出它们的公共部分即可得解.
解答 解:$\left\{\begin{array}{l}{2(m+1.5)≥5①}\\{\frac{5}{2}m<m+3②}\end{array}\right.$
解①得m≥1,
解②得m<2.
故不等式组的解集为1≤m<2.
点评 考查了一元一次不等式组,一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.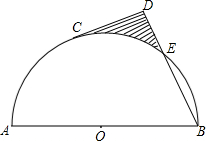 如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
 如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )| A. | 8$\sqrt{3}$-4π | B. | 8$\sqrt{3}$-$\frac{8}{3}$π | C. | 4π-6$\sqrt{3}$ | D. | 6$\sqrt{3}$-$\frac{8}{3}$π |
16.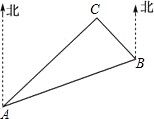 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )| A. | 90° | B. | 80° | C. | 70° | D. | 60° |
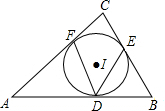 如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.
如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.