题目内容
5.已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.(Ⅰ)如图1,求证ED为⊙O的切线;
(Ⅱ)如图2,直线ED与切线AG相交于G,且OF=1,⊙O的半径为3,求AG的长.
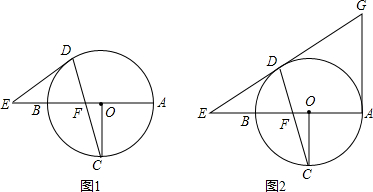
分析 (1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线;
(2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余弦值可得出DM、MO的长度,根据切线的性质可知GA⊥EA,从而得出DM∥GA,根据相似三角形的判定定理即可得出△EDM∽△EGA,根据相似三角形的性质即可得出GA的长度.
解答 (1)证明:连接OD,如图1所示.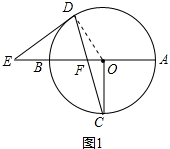
∵ED=EF,
∴∠EDF=∠EFD,
∵∠EFD=∠CFO,
∴∠EDF=∠CFO.
∵OD=OC,
∴∠ODF=∠OCF.
∵OC⊥AB,
∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°,
∴ED为⊙O的切线.
(2)解:连接OD,过点D作DM⊥BA于点M,如图2所示.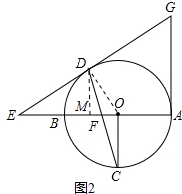
由(1)可知△EDO为直角三角形,设ED=EF=a,EO=EF+FO=a+1,
由勾股定理得:EO2=ED2+DO2,即(a+1)2=a2+32,
解得:a=4,即ED=4,EO=5.
∵sin∠EOD=$\frac{ED}{EO}$=$\frac{4}{5}$,cos∠EOD=$\frac{OD}{EO}$=$\frac{3}{5}$,
∴DM=OD•sin∠EOD=3×$\frac{4}{5}$=$\frac{12}{5}$,MO=OD•cos∠EOD=3×$\frac{3}{5}$=$\frac{9}{5}$,
∴EM=EO-MO=5-$\frac{9}{5}$=$\frac{16}{5}$,EA=EO+OA=5+3=8.
∵GA切⊙O于点A,
∴GA⊥EA,
∴DM∥GA,
∴△EDM∽△EGA,
∴$\frac{GA}{DM}=\frac{EA}{EM}$,
∴GA=$\frac{EA•DM}{EM}$=$\frac{8×\frac{12}{5}}{\frac{16}{5}}$=6.
点评 本题考查了切线的判定、等腰三角形的性质、角的三角函数值、相似三角形的判定及性质,解题的关键是:(1)通过等腰三角形的性质找出∠EDO=90°;(2)通过相似三角形的性质找出相似比.本题属于中档题,难度不大,解决该题型题目时,根据角的计算找出直角,从而证出切线.

 名校课堂系列答案
名校课堂系列答案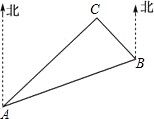 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )| A. | 90° | B. | 80° | C. | 70° | D. | 60° |
①两点确定一条直线;②两点之间,线段最短;③对顶角相等;④内错角相等;
其中真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
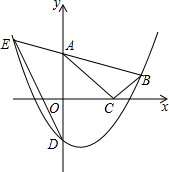 如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.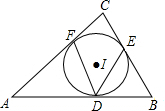 如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.
如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.