题目内容
8.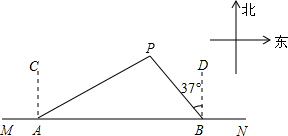 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).
如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).
分析 过点P作PE⊥AB于点E,由题意得,∠PAE=28°,∠PBE=53°,AP=30海里.解Rt△APE,求出PE=30sin28°;再解Rt△BPE,由BP=$\frac{PE}{sin∠PBE}$,代入数据即可.
解答 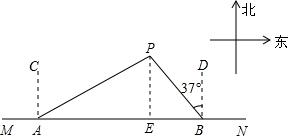 解:如图所示:过点P作PE⊥AB于点E.
解:如图所示:过点P作PE⊥AB于点E.
由题意得,∠PAE=28°,∠PBE=53°,AP=30海里.
在Rt△APE中,PE=APsin∠PAE=30sin28°;
在Rt△BPE中,PE=30sin28°,∠PBE=53°,
则BP=$\frac{PE}{sin∠PBE}$=$\frac{30sin28°}{sin53°}$海里.
点评 本题考查了解直角三角形的应用-方向角问题,解答本题的关键是理解方向角的定义,能利用三角函数值计算有关线段,难度一般.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
16.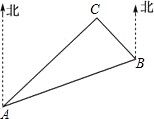 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )| A. | 90° | B. | 80° | C. | 70° | D. | 60° |
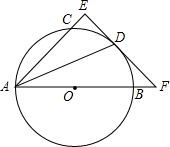 如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.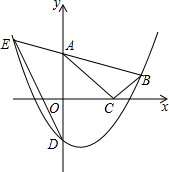 如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.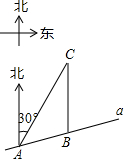 如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.
如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.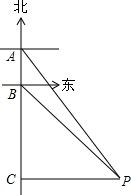 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)