题目内容
 如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.
如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.考点:垂线
专题:
分析:先由点O为直线BD上一点,根据邻补角定义得出∠COD+∠B0C=180°,将∠COD=2∠B0C代入,求出∠B0C=60°,再根据∠1=∠COA-∠BOC即可求解.
解答:解:∵点O为直线BD上一点,
∴∠COD+∠B0C=180°,
将∠COD=2∠B0C代入,
得2∠B0C+∠B0C=180°,
解得∠B0C=60°,
∴∠1=∠COA-∠BOC=90°-60°=30°.
∴∠COD+∠B0C=180°,
将∠COD=2∠B0C代入,
得2∠B0C+∠B0C=180°,
解得∠B0C=60°,
∴∠1=∠COA-∠BOC=90°-60°=30°.
点评:本题考查了邻补角定义,角的和差及角的计算,求出∠B0C=60°是解题的关键.

练习册系列答案
相关题目
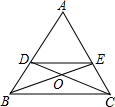 在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )
在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )| A、△OBC是等腰三角形 |
| B、△DBE是等腰三角形 |
| C、△DCE是等腰三角形 |
| D、△ACD是等腰三角形 |
 如图,已知菱形ABCD中,对角线AC、BD交于O点,AB=10,BD=12,则AC=
如图,已知菱形ABCD中,对角线AC、BD交于O点,AB=10,BD=12,则AC=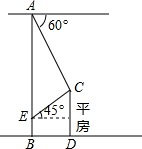 如图,已知楼AB高25米,从楼顶A处测得对面小平房C的俯角为60°,又乘电梯到离地5米的一窗户E处测得小平房顶C的仰角为45°,则小平房到大楼的距离为
如图,已知楼AB高25米,从楼顶A处测得对面小平房C的俯角为60°,又乘电梯到离地5米的一窗户E处测得小平房顶C的仰角为45°,则小平房到大楼的距离为 如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.
如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.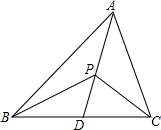 如图,在△ABC中,AB>AC>BC,P为三角形内任意一点,连接AP,并延长交BC于D.求证:
如图,在△ABC中,AB>AC>BC,P为三角形内任意一点,连接AP,并延长交BC于D.求证: