题目内容
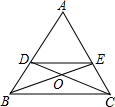 在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )
在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )| A、△OBC是等腰三角形 |
| B、△DBE是等腰三角形 |
| C、△DCE是等腰三角形 |
| D、△ACD是等腰三角形 |
考点:等腰三角形的判定与性质
专题:
分析:根据等腰三角形的性质和角平分线的定义得出相等的角,即可证出等腰三角形.
解答:解:∵AB=AC,
∴∠ABC=∠ACB,
∵BE、CD分别是∠ABC、ACB的平分线,
∴∠ABE=∠CBE=
∠ABC,∠ACD=∠BCD=
∠ACB,
∴∠CBE=∠BCD,
∴△OBC是等腰三角形,
∴A正确;
∵∠ABE=∠ACD,AB=AC,∠A=∠A,
∴△ABE≌△ACD,
∴AD=AE,
∴
=
,
∴DE∥BC,
∴∠DEB=∠CBE,∠EDC=∠BCD,
∴∠ABE=∠DEB,∠EDC=∠ACD,
∴BD=ED,CE=ED,
∴△DBE、△DCE是等腰三角形;
∴B、C正确.
故选:D.
∴∠ABC=∠ACB,
∵BE、CD分别是∠ABC、ACB的平分线,
∴∠ABE=∠CBE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBE=∠BCD,
∴△OBC是等腰三角形,
∴A正确;
∵∠ABE=∠ACD,AB=AC,∠A=∠A,
∴△ABE≌△ACD,
∴AD=AE,
∴
| AD |
| AB |
| AE |
| AC |
∴DE∥BC,
∴∠DEB=∠CBE,∠EDC=∠BCD,
∴∠ABE=∠DEB,∠EDC=∠ACD,
∴BD=ED,CE=ED,
∴△DBE、△DCE是等腰三角形;
∴B、C正确.
故选:D.
点评:本题考查了等腰三角形的判定和角平分线的性质;由等腰三角形的两个底角相等和角平分线的定义证出相等的角是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,△ABC经过平移后得到△DEF,则和BC相等的线段是( )
如图,△ABC经过平移后得到△DEF,则和BC相等的线段是( )| A、EC | B、EF | C、CF | D、DE |
如果a=(-99)0,b=(-0.1)-1,c=(-
)-2,那么a,b,c三数的大小为( )
| 2 |
| 3 |
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
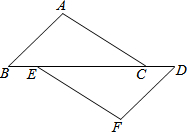 如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是:
如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是: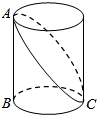 如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 如图,在?ABCD中,AB=BK,直线KD与BC交于点E.求证:△ADK的周长为△ECD周长的两倍.
如图,在?ABCD中,AB=BK,直线KD与BC交于点E.求证:△ADK的周长为△ECD周长的两倍. 如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.
如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.