题目内容
设2y-3x=0(y≠0),则
= .
| x+y |
| y |
考点:比例的性质
专题:
分析:先由2y-3x=0(y≠0),可得3x=2y,根据比例的基本性质得出
=
,因而可以设y=3k,则x=2k.代入求出
的值.
| y |
| x |
| 3 |
| 2 |
| x+y |
| y |
解答:解:∵2y-3x=0(y≠0),
∴3x=2y,
∴
=
,
∴可设y=3k,则x=2k,
∴
=
=
.
故答案为
.
∴3x=2y,
∴
| y |
| x |
| 3 |
| 2 |
∴可设y=3k,则x=2k,
∴
| x+y |
| y |
| 2k+3k |
| 3k |
| 5 |
| 3 |
故答案为
| 5 |
| 3 |
点评:本题考查了比例的基本性质:两内项之积等于两外项之积.如果已知几个量的比值时,常用的解法是:设一个未知数,把题目中的几个量用所设的未知数表示出来,实现消元.

练习册系列答案
相关题目
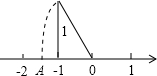 如图,数轴上的点A所表示的数为( )
如图,数轴上的点A所表示的数为( )A、
| ||
B、-
| ||
C、
| ||
D、1-
|
 如图,A、B、C是⊙O上的点,∠ACB=32°,则∠AOB等于( )
如图,A、B、C是⊙O上的点,∠ACB=32°,则∠AOB等于( )| A、16° | B、64° |
| C、148° | D、32° |
已知等腰三角形的一个外角等于110°,则该三角形的一个底角是( )
| A、35° |
| B、70°或110° |
| C、70° |
| D、55°或70° |
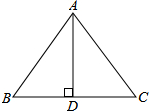 如图,在等腰△ABC中,AD是底边BC上的高,AB=AC=5,BC=6,P是线段AD上一个动点,记AP长为x,当A在以P为圆心,PB为半径的圆的外部时,求x的取值范围.
如图,在等腰△ABC中,AD是底边BC上的高,AB=AC=5,BC=6,P是线段AD上一个动点,记AP长为x,当A在以P为圆心,PB为半径的圆的外部时,求x的取值范围. 如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.
如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数. 如图,一天晚上身高1.8米的李明在广场上散步,他从距路灯的底部O点10米的A点沿OA方向行走26米到C点处,李明在A处时,头顶B在路灯下形成的影子在点M处,已知灯杆垂直于路面.
如图,一天晚上身高1.8米的李明在广场上散步,他从距路灯的底部O点10米的A点沿OA方向行走26米到C点处,李明在A处时,头顶B在路灯下形成的影子在点M处,已知灯杆垂直于路面.