题目内容
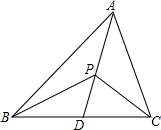 如图,在△ABC中,AB>AC>BC,P为三角形内任意一点,连接AP,并延长交BC于D.求证:
如图,在△ABC中,AB>AC>BC,P为三角形内任意一点,连接AP,并延长交BC于D.求证:(1)AB+AC>AD+BC;
(2)AB+AC>AP+BP+CP.
考点:三角形三边关系
专题:证明题
分析:(1)根据大边对大角和等量关系可得∠ABC<∠ADB,再根据大角对大边可得AB>AD,再根据等量关系即可求解;
(2)把△BCP绕点C逆时针旋转60°,得到△CEF,则PC=PF,FE=BP,EC=BC,再根据等量关系即可得到AB+AC>AP+BP+CP.
(2)把△BCP绕点C逆时针旋转60°,得到△CEF,则PC=PF,FE=BP,EC=BC,再根据等量关系即可得到AB+AC>AP+BP+CP.
解答: 证明:(1)∵AB>AC,
证明:(1)∵AB>AC,
∴∠ABC<∠ACB,
∵∠ACB<∠ADB,
∴∠ABC<∠ADB,
∴AB>AD,
∵AC>BC,
∴AB+AC>AD+BC;
(2)如图,把△BCP绕点C逆时针旋转60°,
得到△CEF,则PC=PF,FE=BP,EC=BC.
∵AC+EC>AE=PA+PF+FE,AB>BC,
∴AB+AC>PA+BP+PC.
 证明:(1)∵AB>AC,
证明:(1)∵AB>AC,∴∠ABC<∠ACB,
∵∠ACB<∠ADB,
∴∠ABC<∠ADB,
∴AB>AD,
∵AC>BC,
∴AB+AC>AD+BC;
(2)如图,把△BCP绕点C逆时针旋转60°,
得到△CEF,则PC=PF,FE=BP,EC=BC.
∵AC+EC>AE=PA+PF+FE,AB>BC,
∴AB+AC>PA+BP+PC.
点评:本题考查了三角形三边关系定理:三角形两边之和大于第三边.三角形的性质:大边对大角,大角对大边.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
下列方程是关于x的一元二次方程的是( )
| A、x2+2x-3=x2 | ||
B、x-
| ||
| C、x(x-1)=x | ||
| D、3x2+y+1=0 |
 由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是
由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是 如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.
如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数. 如图,一天晚上身高1.8米的李明在广场上散步,他从距路灯的底部O点10米的A点沿OA方向行走26米到C点处,李明在A处时,头顶B在路灯下形成的影子在点M处,已知灯杆垂直于路面.
如图,一天晚上身高1.8米的李明在广场上散步,他从距路灯的底部O点10米的A点沿OA方向行走26米到C点处,李明在A处时,头顶B在路灯下形成的影子在点M处,已知灯杆垂直于路面.