题目内容
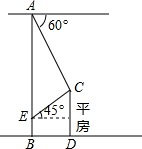 如图,已知楼AB高25米,从楼顶A处测得对面小平房C的俯角为60°,又乘电梯到离地5米的一窗户E处测得小平房顶C的仰角为45°,则小平房到大楼的距离为
如图,已知楼AB高25米,从楼顶A处测得对面小平房C的俯角为60°,又乘电梯到离地5米的一窗户E处测得小平房顶C的仰角为45°,则小平房到大楼的距离为考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先过点C作CF⊥AB于F,易证四边形EFCG与四边形BEGD是矩形,设CG=xm,在Rt△CEG和Rt△AFC中,根据角的度数表示出AF,EF的长,又由楼AB的高为25米,列出方程,求出x的值,即可得出答案.
解答: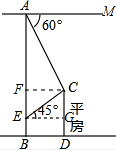 解:过点C作CF⊥AB于F,
解:过点C作CF⊥AB于F,
∴CF∥EG∥AM,
∴∠MAC=∠ACF=60°,
∴四边形EFCG与四边形BEGD是矩形,
∴EF=CG,DG=BE=5,FC=EG,
设CG=xm,
∴EF=CG=xm,
在Rt△CEG中,∠CGE=90°,∠CEG=45°,
∴CG=EG=CF=EF=x(m),
在Rt△AFC中,AF=FC•tan60°=
x(m),
∵AB=25m,
∴
x+x+5=25,
解得:x=10(
-1)=10
-10,
∴AF=
x=
×(10
-10)=30-10
(m).
答:小平房到大楼的距离为(30-10
)m.
故答案为:30-10
.
 解:过点C作CF⊥AB于F,
解:过点C作CF⊥AB于F,∴CF∥EG∥AM,
∴∠MAC=∠ACF=60°,
∴四边形EFCG与四边形BEGD是矩形,
∴EF=CG,DG=BE=5,FC=EG,
设CG=xm,
∴EF=CG=xm,
在Rt△CEG中,∠CGE=90°,∠CEG=45°,
∴CG=EG=CF=EF=x(m),
在Rt△AFC中,AF=FC•tan60°=
| 3 |
∵AB=25m,
∴
| 3 |
解得:x=10(
| 3 |
| 3 |
∴AF=
| 3 |
| 3 |
| 3 |
| 3 |
答:小平房到大楼的距离为(30-10
| 3 |
故答案为:30-10
| 3 |
点评:本题考查仰角与俯角的定义,能借助仰角与俯角构造直角三角形并解直角三角形是解此题的关键,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=9,BC=12,点E是BC的中点,点F是CD边上的任意一点,当△AEF的周长最小时,DF=
如图,在矩形ABCD中,AB=9,BC=12,点E是BC的中点,点F是CD边上的任意一点,当△AEF的周长最小时,DF= 由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是
由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是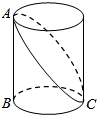 如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为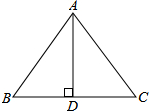 如图,在等腰△ABC中,AD是底边BC上的高,AB=AC=5,BC=6,P是线段AD上一个动点,记AP长为x,当A在以P为圆心,PB为半径的圆的外部时,求x的取值范围.
如图,在等腰△ABC中,AD是底边BC上的高,AB=AC=5,BC=6,P是线段AD上一个动点,记AP长为x,当A在以P为圆心,PB为半径的圆的外部时,求x的取值范围. 如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.
如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.