题目内容
(1)【操作发现】如图①,在矩形ABCD中,E是BC中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,连接FC,猜想∠GFC与∠GCF的关系,并证明你的结论.
(2)【类比探究】如图②,将(1)中的矩形ABCD改为平行四边形,其他条件不变,(1)中的结论是否仍然成立?请说明理由.
(3)【应用】若满足(2)中条件,且∠AGD=140°,则∠FCG= .
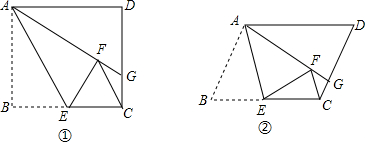
(2)【类比探究】如图②,将(1)中的矩形ABCD改为平行四边形,其他条件不变,(1)中的结论是否仍然成立?请说明理由.
(3)【应用】若满足(2)中条件,且∠AGD=140°,则∠FCG=

考点:翻折变换(折叠问题),平行四边形的性质,矩形的性质
专题:
分析:(1)如图①,首先证明∠AFE=∠ECG=90°,EF=EC;进而得到∠EFC=∠ECF,即可解决问题.
(2)如图②,首先证明∠EFC=∠ECF,其次证明∠EFG=∠ECG,即可解决问题.
(3)运用(2)中的结论,结合外角定理,即可解决问题.
(2)如图②,首先证明∠EFC=∠ECF,其次证明∠EFG=∠ECG,即可解决问题.
(3)运用(2)中的结论,结合外角定理,即可解决问题.
解答: 解:(1)∠GFC=∠GCF;理由如下:
解:(1)∠GFC=∠GCF;理由如下:
如图1,∵四边形ABCD为矩形,
∴∠B=∠ECG=90°;
由题意得:BE=CE,BE=EF,∠AFE=∠B,
∴∠AFE=∠ECG=90°,EF=EC,
∴∠EFC=∠ECF(设为α),
∴∠GFC=∠GCF=90°-α.
(2)(1)中的结论仍然成立;理由如下:
∵四边形ABCD为平行四边形,
∴∠B+∠ECG=180°;
由题意得:BE=CE,BE=EF,∠AFE=∠B(设为α),
∴∠AFE=∠ECG=180°-α,EF=EC,
∴∠EFC=∠ECF;
∵∠EFG=180°-α,∠ECG=180°-α,
∴∠EFG=∠ECG,
∴∠GFC=∠GCF.
(3)∵∠AGD=∠GFC+∠FCG,且∠AGD=140°,
∴∠FCG=70°.
故答案为:70°.
 解:(1)∠GFC=∠GCF;理由如下:
解:(1)∠GFC=∠GCF;理由如下:如图1,∵四边形ABCD为矩形,
∴∠B=∠ECG=90°;
由题意得:BE=CE,BE=EF,∠AFE=∠B,
∴∠AFE=∠ECG=90°,EF=EC,
∴∠EFC=∠ECF(设为α),
∴∠GFC=∠GCF=90°-α.
(2)(1)中的结论仍然成立;理由如下:
∵四边形ABCD为平行四边形,
∴∠B+∠ECG=180°;
由题意得:BE=CE,BE=EF,∠AFE=∠B(设为α),
∴∠AFE=∠ECG=180°-α,EF=EC,
∴∠EFC=∠ECF;
∵∠EFG=180°-α,∠ECG=180°-α,
∴∠EFG=∠ECG,
∴∠GFC=∠GCF.
(3)∵∠AGD=∠GFC+∠FCG,且∠AGD=140°,
∴∠FCG=70°.
故答案为:70°.
点评:该题主要考查了翻折变换的性质、平行四边形的性质、矩形的性质等几何知识点及其应用问题;解题的关键是牢固掌握翻折变换的性质、平行四边形的性质、矩形的性质等几何知识点.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
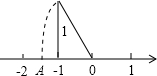 如图,数轴上的点A所表示的数为( )
如图,数轴上的点A所表示的数为( )A、
| ||
B、-
| ||
C、
| ||
D、1-
|
 如图,OM平分∠AOB,ON平分∠BOC,∠AOC=120°,则∠MON=
如图,OM平分∠AOB,ON平分∠BOC,∠AOC=120°,则∠MON= 如图,在矩形ABCD中,AB=9,BC=12,点E是BC的中点,点F是CD边上的任意一点,当△AEF的周长最小时,DF=
如图,在矩形ABCD中,AB=9,BC=12,点E是BC的中点,点F是CD边上的任意一点,当△AEF的周长最小时,DF=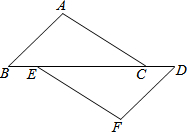 如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是:
如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是: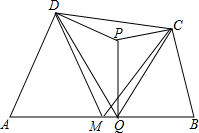 如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.
如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD. 由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是
由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是 如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.
如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.