题目内容
 如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.
如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.考点:锐角三角函数的定义,坐标与图形性质
专题:
分析:过P作PA⊥x轴于A,PB⊥y轴于B,由P点的坐标可知,OA=PB=3,OB=PA=4,再根据锐角三角函数的定义解答.
解答: 解:过P作PA⊥x轴于A,PB⊥y轴于B,
解:过P作PA⊥x轴于A,PB⊥y轴于B,
∵P点坐标为(3,4),
∴OA=PB=3,OB=PA=4,
∴tanα=
=
,
tanβ=
=
.
 解:过P作PA⊥x轴于A,PB⊥y轴于B,
解:过P作PA⊥x轴于A,PB⊥y轴于B,∵P点坐标为(3,4),
∴OA=PB=3,OB=PA=4,
∴tanα=
| PA |
| OA |
| 4 |
| 3 |
tanβ=
| PB |
| OB |
| 3 |
| 4 |
点评:本题考查的是锐角三角函数的定义,坐标与图形性质,过P点作PA⊥x轴于A,PB⊥y轴于B,构造出直角三角形是解答此题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 如图,△ABC经过平移后得到△DEF,则和BC相等的线段是( )
如图,△ABC经过平移后得到△DEF,则和BC相等的线段是( )| A、EC | B、EF | C、CF | D、DE |
下列条件中能判定△ABC≌△DEF的是( )
| A、∠B=∠E,∠C=∠F,AC=DF |
| B、∠A=∠D,∠B=∠E,∠C=∠F |
| C、AC=DF,∠B=∠F,AB=DE |
| D、AB=DE,BC=EF,∠A=∠D |
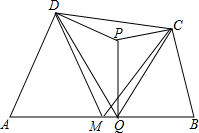 如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.
如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.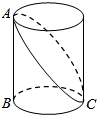 如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.
如图,点O为直线BD上一点,∠COA=90°,∠COD=2∠B0C,求∠1的度数.