题目内容
13.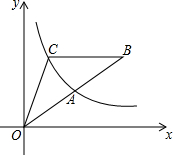 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,B是直线OA上的一点,且OA=AB,过点B作x轴的平行线交曲线y=$\frac{k}{x}$于点C,连OC,若S△ABC=9,那么k的值等于6.
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,B是直线OA上的一点,且OA=AB,过点B作x轴的平行线交曲线y=$\frac{k}{x}$于点C,连OC,若S△ABC=9,那么k的值等于6.
分析 由OA=AB,S△ABC=9可知S△BOC=18,设A(a,$\frac{k}{a}$),根据已知条件得出B(2a,$\frac{2k}{a}$),进一步得出C($\frac{1}{2}$a,$\frac{2k}{a}$),然后根据S△BOC=$\frac{1}{2}$BC•$\frac{2k}{a}$得出=$\frac{1}{2}$(2a-$\frac{1}{2}$a)•$\frac{2k}{a}$=18,解方程即可求得.
解答 解:设A(a,$\frac{k}{a}$),
∵OA=AB,
∴B(2a,$\frac{2k}{a}$),
∴C的纵坐标为$\frac{2k}{a}$,
代入y=$\frac{k}{x}$得,$\frac{2k}{a}$=$\frac{k}{x}$,
解得x=$\frac{1}{2}$a,
∴C($\frac{1}{2}$a,$\frac{2k}{a}$),
∵S△ABC=9,OA=AB,
∴S△BOC=18,
∵S△BOC=$\frac{1}{2}$BC•$\frac{2k}{a}$=$\frac{1}{2}$(2a-$\frac{1}{2}$a)•$\frac{2k}{a}$=18,
解得k=6,
故答案为6.
点评 本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,根据题意表示出B、C的坐标是解题的关键.

练习册系列答案
相关题目
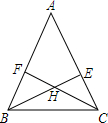 已知:如图,BE和CF是△ABC的高线,BE=CF,H是CF、BE的交点.求证:HB=HC.
已知:如图,BE和CF是△ABC的高线,BE=CF,H是CF、BE的交点.求证:HB=HC.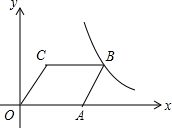 如图,?OABC的边OA在x轴上,C(1,2),A(3,0),双曲线y=$\frac{k}{x}$(x>0)经过点B,求k的值.
如图,?OABC的边OA在x轴上,C(1,2),A(3,0),双曲线y=$\frac{k}{x}$(x>0)经过点B,求k的值.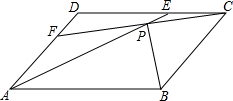 在?ABCD的两边AD,CD上各取一点F,E,连接AE,CF交于点P,且AE=CF.求证:PB平分∠APC.
在?ABCD的两边AD,CD上各取一点F,E,连接AE,CF交于点P,且AE=CF.求证:PB平分∠APC.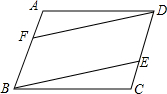 如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.
如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.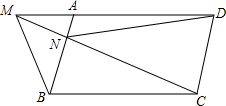 已知M是?ABCD的DA边的延长线上任一点,连结MC交AB于N,求证:S△MNB=S△AND.
已知M是?ABCD的DA边的延长线上任一点,连结MC交AB于N,求证:S△MNB=S△AND.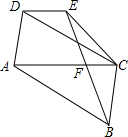 如图,在?ABCD中,过点B作BE交对角线AC于点F,且BF=EF,连接DE、CE,求证:AC∥DE.
如图,在?ABCD中,过点B作BE交对角线AC于点F,且BF=EF,连接DE、CE,求证:AC∥DE.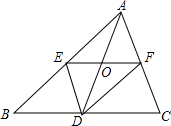 如图,在△ABC中,EF为△ABC的中位线,D为BC边上的中点,AD与EF交于点O,连结EF、DF.求证:四边形AEDF为平行四边形.
如图,在△ABC中,EF为△ABC的中位线,D为BC边上的中点,AD与EF交于点O,连结EF、DF.求证:四边形AEDF为平行四边形.