题目内容
3．
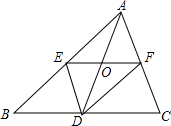如图，在△ABC中，EF为△ABC的中位线，D为BC边上的中点，AD与EF交于点O，连结EF、DF．求证：四边形AEDF为平行四边形．
分析 根据中位线定理和平行四边形的判定定理进行证明即可．
解答 证明：∵EF为△ABC的中位线，
∴CF=AF，AE=$\frac{1}{2}$AB．
∵BD=CD，
∴点D是BC的中点，DF是中位线．
∴DF=$\frac{1}{2}$AB，DF∥AB
∴DF$\stackrel{∥}{=}$AE，
∴四边形AEDF为平行四边形．
点评 本题三角形的中位线的性质考查了平行四边形的判定：三角形的中位线平行于第三边，且等于第三边的一半．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
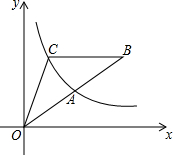如图，点A是反比例函数y=$\frac{k}{x}$的图象上的一点，B是直线OA上的一点，且OA=AB，过点B作x轴的平行线交曲线y=$\frac{k}{x}$于点C，连OC，若S△ABC=9，那么k的值等于6．
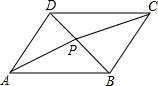如图，点P是?ABCD内的一点，连结AP，BP，CP，DP，若△APB的面积为40cm2，△BPC的面积为25cm2，△CPD的面积为15cm2，则根据题目中所给的条件，能求出△PAD的面积吗？如果能，请你求出△PAD的面积；如果不能，请你说明理由．
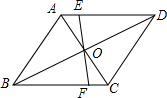如图，点O是菱形ABCD对角线的交点，过O点的直线AD、BC于点E、F．求证：AE+BF=AB．
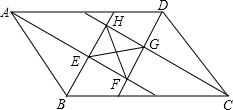如图，在?ABCD中，四个内角的平分线分别相交于点E，F，G，H．
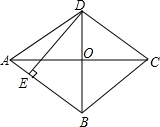如图，菱形ABCD中，对角线AC、BD相交于点O，DE⊥AB于点E，若菱形的周长为8$\sqrt{13}$，tan∠OAD=$\frac{2}{3}$，求DE的长．