题目内容
8．
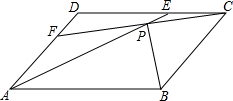在?ABCD的两边AD，CD上各取一点F，E，连接AE，CF交于点P，且AE=CF．求证：PB平分∠APC．
分析 连接BE，BF，过B作BN⊥CF，BM⊥AE，根据平行四边形的面积可得S△ABE=S△BFC=$\frac{1}{2}$S平行四边形ABCD，根据三角形的面积可得$\frac{1}{2}$•AE×BM=$\frac{1}{2}$CF•BN，再由条件AE=CF可得BM=BN，根据到角两边距离相等的点在角的平分线上可得结论．
解答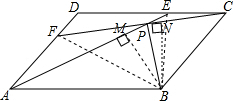 
证明：连接BE，BF，过B作BN⊥CF，BM⊥AE，
∵四边形ABCD是平行四边形，
∴S△ABE=S△BFC=$\frac{1}{2}$S平行四边形ABCD，
∴$\frac{1}{2}$•AE×BM=$\frac{1}{2}$CF•BN，
∵AE=CF，
∴BM=BN，
∴PB平分∠APC．
点评 此题主要考查了平行四边形的性质，以及角平分线的判定，关键是掌握平行四边形的面积公式，正确作出辅助线．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
在边长为1的小正方形网格中，△AOB的顶点均在格点上，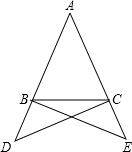
如图，在△ABC中，AB=AC，点D、E分别在AB、AC的延长线上，且∠BCD=$\frac{1}{3}$∠ACB，∠CBE=$\frac{1}{3}$∠ABC．求证：BE=CD．
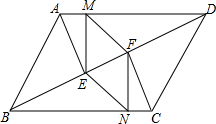已知，在?ABCD中，AE⊥BD，CF⊥BD，E、F为垂足，EM⊥AD，FN⊥BC，M、N为垂足．求证：MF∥EN，MF=EN．
如图，在?ABCD中，AB=2BC，E为AB的中点，DF⊥BC，垂足为F．请你说明：∠AED=∠EFB．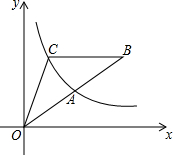
如图，点A是反比例函数y=$\frac{k}{x}$的图象上的一点，B是直线OA上的一点，且OA=AB，过点B作x轴的平行线交曲线y=$\frac{k}{x}$于点C，连OC，若S△ABC=9，那么k的值等于6．
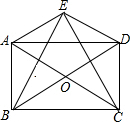如图，点E为?ABCD外一点，AE⊥EC，BE⊥ED，对角线AC、BD相交于点O．
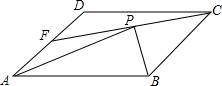在平行四边形ABCD中，F是AD的中点，BP⊥CF交于点P，若AP=2$\sqrt{3}$，求AB的长．
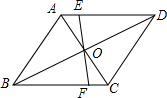如图，点O是菱形ABCD对角线的交点，过O点的直线AD、BC于点E、F．求证：AE+BF=AB．