题目内容
15.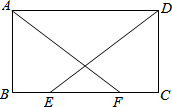 如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.(1)求证:△ABF≌△DCE;
(2)若∠BFA=40°,求∠BAF的度数.
分析 (1)由平行四边形的性质得出AB=DC,证出BF=CE,由SSS证明△ABF≌△DCE即可;
(2)由全等三角形的性质得出∠B=∠C,由平行四边形的性质得出∠B+∠C=180°,得出∠B=90°,由角的互余关系即可得出∠BAF的度数.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∵BE=CF,
∴BF=CE,
在△ABF和△DCE中,$\left\{\begin{array}{l}{AB=DC}&{\;}\\{BF=CE}&{\;}\\{AF=DE}&{\;}\end{array}\right.$,
∴△ABF≌△DCE(SSS);
(2)解:∵△ABF≌△DCE,
∴∠B=∠C,
∵AB∥DC,
∴∠B+∠C=180°,
∴∠B=90°,
∴∠BAF=90°-∠BFA=90°-40°=50°.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、直角三角形的性质;熟练掌握平行四边形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
20.某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了3782张相片.若全班有x名学生,根据题意,列出方程为( )
| A. | x(x-1)=3782 | B. | $\frac{x(x-1)}{2}$=3782 | C. | 2x(x-1)=3782 | D. | x(x+1)=3782 |
5.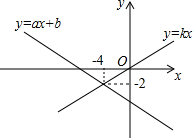 已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
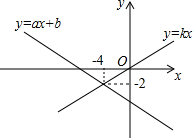 已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )
已知如图y=ax+b与y=kx的图象交于点P,则根据图象可得不等式kx>ax+b的解是( )| A. | x>-4 | B. | x<-2 | C. | x<-4 | D. | x>-2 |
 如图,D是△ABC的边AB上一点,已知AC2=AD•AB,求证:∠ACD=∠ABC.
如图,D是△ABC的边AB上一点,已知AC2=AD•AB,求证:∠ACD=∠ABC. 如图,AB=AC,∠A=50°,AC的垂直平分线MN交AB于D.求∠BCD的度数?
如图,AB=AC,∠A=50°,AC的垂直平分线MN交AB于D.求∠BCD的度数?