题目内容
10. 如图,D是△ABC的边AB上一点,已知AC2=AD•AB,求证:∠ACD=∠ABC.
如图,D是△ABC的边AB上一点,已知AC2=AD•AB,求证:∠ACD=∠ABC.
分析 由对应边成比例,及夹角可得△ACD∽△ABC,根据相似三角形的性质可知对应角相等.
解答 解:∵AC2=AD•AB,即$\frac{AC}{AD}$=$\frac{AB}{AC}$,又∠A为公共角,
∴△ACD∽△ABC,
∴∠ACD=∠ABC.
点评 本题主要考查相似三角形的判定和性质,掌握利用两组角对应相等可判定两个三角形相似是解题的关键,把线段的乘积化为比例来证明是解这类问题的一般思路.

练习册系列答案
相关题目
1.设a<b,下列不等式变形错误的是( )
| A. | a-12<b-12 | B. | a+7<b+7 | C. | -12a<-12b | D. | 7a<7b |
19. 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
20.下列判断正确的是( )
| A. | 点(-2,6)与点(2,6)关于x轴对称 | B. | 点(2,-6)与点(-2,6)关于y轴对称 | ||
| C. | 点(2,6)与点(2,-6)关于x轴对称 | D. | 点(2,-6)与点(6,2)关于y轴对称 |
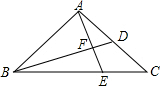 如图,在△ABC中,BD为AC边上的中线,BE=AB,且AE与BD相交于点F,求证:$\frac{AB}{BC}$=$\frac{EF}{AF}$.
如图,在△ABC中,BD为AC边上的中线,BE=AB,且AE与BD相交于点F,求证:$\frac{AB}{BC}$=$\frac{EF}{AF}$.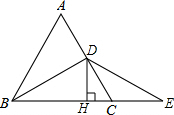 如图,在等腰△ABC中,AB=AC,BD为∠ABC平分线,延长BC到点E,使CE=CD,作DH⊥BE于H,求证:H为BE的中点.
如图,在等腰△ABC中,AB=AC,BD为∠ABC平分线,延长BC到点E,使CE=CD,作DH⊥BE于H,求证:H为BE的中点.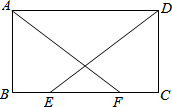 如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.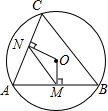 如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC垂足分别为M、N,如果MN=6,那么BC=12.
如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC垂足分别为M、N,如果MN=6,那么BC=12.