题目内容
4. 如图,AB=AC,∠A=50°,AC的垂直平分线MN交AB于D.求∠BCD的度数?
如图,AB=AC,∠A=50°,AC的垂直平分线MN交AB于D.求∠BCD的度数?
分析 根据等腰三角形的性质和三角形内角和定理求出∠ACB的度数,根据线段的垂直平分线的性质得到DC=DA,由等腰三角形的性质得到∠ACD=∠A,计算即可.
解答 解:∵AB=AC,∠A=50°,
∴∠ACB=∠B=65°,
∵DE的线段AC的垂直平分线,
∴DC=DA,
∴∠ACD=∠A=50°,
∴∠BCD=∠ACB-∠ACD=15°.
答:∠BCD的度数是15°.
点评 本题考查的是线段的垂直平分线的性质和三角形内角和定理,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
19. 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
14.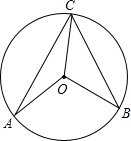 如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
 如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
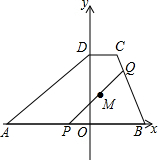 如图,在平面直角坐标系中,四边形ABCD的顶点A、B在x轴上,点D在y轴上,AB∥CD,直线BC表达式为y=-$\frac{4}{3}$x+16,点A、D的坐标分别为(-16,0)、(0,12),动点P从点A出发沿AB方向,动点Q从点B出发沿四边形ABCD边BC-CD-DA方向,同时开始运动,速度均为每秒1个单位.当P点到达B点时两个动点同时停止运动,设运动时间为t.
如图,在平面直角坐标系中,四边形ABCD的顶点A、B在x轴上,点D在y轴上,AB∥CD,直线BC表达式为y=-$\frac{4}{3}$x+16,点A、D的坐标分别为(-16,0)、(0,12),动点P从点A出发沿AB方向,动点Q从点B出发沿四边形ABCD边BC-CD-DA方向,同时开始运动,速度均为每秒1个单位.当P点到达B点时两个动点同时停止运动,设运动时间为t.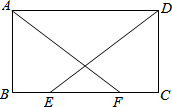 如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE. 如图是几何体的三视图及相关数据(单位:cm),则该几何体的全面积为3πcm2.
如图是几何体的三视图及相关数据(单位:cm),则该几何体的全面积为3πcm2.