题目内容

18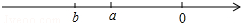．已知：表示a、b两个实数的点在数轴上的位置如图所示，化简|a-b|+$\sqrt{（a+b）^{2}}$=-2b．

分析 直接利用二次根式的性质$\sqrt{a}$=|a|，再结合绝对值的性质分别化简，进而得出答案．

解答 解：由数轴可得：a-b＞0，a+b＜0，
故|a-b|+$\sqrt{（a+b）^{2}}$=a-b-（a+b）=-2b．
故答案为：-2b．

点评 此题主要考查了二次根式的性质与化简以及绝对值的性质，正确掌握二次根式的性质是解题关键．

练习册系列答案
相关题目
8．计算：
（1）x2•x3+（x2）4÷x3
（2）（x+y）2-（x-y）2．
9．若（x+a）2=x2+bx+25，则a，b分别为（　　）
A．a=3，b=6B．a=5，b=5或a=-5，b=-10
C．a=5，b=10D．a=-5，b=-10或a=5，b=10
6．已知4x2-mxy+9y2是关于x，y的完全平方式，则m=±12．
13．（1）约分  $\frac{{{x^2}-{y^2}}}{{{x^2}-xy}}$
（2）通分  $\frac{2}{{{x^2}-x}}$，$\frac{1}{{{x^2}-1}}$．
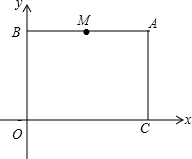3．平面直角坐标系中，O是坐标原点，点A是第一象限内一点，A（m，n）满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线，交y轴于点B，交x轴于点C．M是线段AB的中点，点P从M点出发沿线段MA-AC向终点C运动，速度为每秒2个单位长度．设点P运动的时间为t（秒）．
（1）求出A点坐标．
（2）用含有t的代数式表示线段AP的长度．
（3）作线段OP、PM、OM，当三角形MOP的面积等于直角梯形AMOC的面积的$\frac{1}{2}$时，求t的值，并求出此时点P的坐标．
10．如果要使关于x的方程$\frac{x}{x-3}$+1-3m=$\frac{m}{x-3}$有唯一解，那么m的取值范围是m≠$\frac{2}{3}$且m≠3．
7．数轴上点A、B分别表示实数1、$\sqrt{5}$-1，则A、B两点间的距离为$\sqrt{5}$-2．
8．下列计算正确的是（　　）
A．3x2-4x2=-1B．3x+x=3x2C．4x•x=4x2D．-4x6÷2x2=-2x3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网