题目内容
3.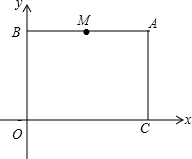 平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C.M是线段AB的中点,点P从M点出发沿线段MA-AC向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t(秒).
平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C.M是线段AB的中点,点P从M点出发沿线段MA-AC向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t(秒).(1)求出A点坐标.
(2)用含有t的代数式表示线段AP的长度.
(3)作线段OP、PM、OM,当三角形MOP的面积等于直角梯形AMOC的面积的$\frac{1}{2}$时,求t的值,并求出此时点P的坐标.
分析 (1)解方程组求出方程组的解,即可得出答案;
(2)分为两种情况:当P在AM上时,当P在AC上时,求出AP即可;
(3)分为两种情况:当P在AM上时,当P在AC上时,分别求出△MOP和四边形AMOC的面积,即可得出关于t的方程,求出t,即可得出答案.
解答 解:(1)解方程组$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$得:$\left\{\begin{array}{l}{m=8}\\{n=6}\end{array}\right.$,
即A的坐标为(8,6);
(2)∵根据题意知:四边形OBAC是矩形,A(8,6),M为AB的中点,
∴OB=AC=6,AB=OC=8,AM=BM=4,
当P在MA上时,AP=4-2t;
当P在AC上时,AP=2t-4;
(3)
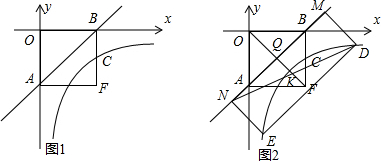
当P在AM上时,如图1,
∵当三角形MOP的面积等于直角梯形AMOC的面积的$\frac{1}{2}$,
∴$\frac{1}{2}$•2t•6=$\frac{1}{2}$×$\frac{1}{2}$×(4+8)×6,
解得:t=3,当t=3时,MP=6>AM,此时不符合P在AM上,舍去;
当P在AC上时,如图2,
∵S△OMP=S四边形AMOC-S△AMP-S△OPC=$\frac{1}{2}$×(4+8)×6-$\frac{1}{2}$×4×(2t-4)-$\frac{1}{2}$×(4+6-2t)×8=4+4t,
S四边形AMOC=$\frac{1}{2}×$(4+8)×6=36,
∴4+4t=$\frac{1}{2}$×36,
解得:t=$\frac{7}{2}$,
AP=2t-4=3,CP=6-3=3,
P点的坐标为(8,3).
点评 本题考查了坐标与图形性质,解二元一次方程组,矩形的性质,三角形的面积等知识点的应用,能进行分类讨论是解此题的关键.

 应用题作业本系列答案
应用题作业本系列答案| A. | $\left\{\begin{array}{l}{x+y=34}\\{x+1=2y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=34}\\{x=2y+1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=34}\\{2x=y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+2y=34}\\{x=2y+1}\end{array}\right.$ |
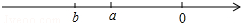 已知:表示a、b两个实数的点在数轴上的位置如图所示,化简|a-b|+$\sqrt{(a+b)^{2}}$=-2b.
已知:表示a、b两个实数的点在数轴上的位置如图所示,化简|a-b|+$\sqrt{(a+b)^{2}}$=-2b.