题目内容
13.(1)约分 $\frac{{{x^2}-{y^2}}}{{{x^2}-xy}}$(2)通分 $\frac{2}{{{x^2}-x}}$,$\frac{1}{{{x^2}-1}}$.
分析 (1)先将原分式的分子和分母能因式分解的先因式分解,然后约分即可解答本题;
(2)找出两个分式的最简公分母即可对两个分式通分.
解答 解;(1)$\frac{{{x^2}-{y^2}}}{{{x^2}-xy}}$
=$\frac{(x+y)(x-y)}{x(x-y)}$
=$\frac{x+y}{x}$;
(2)$\frac{2}{{{x^2}-x}}$,$\frac{1}{{{x^2}-1}}$
$\frac{2}{{x}^{2}-x}$=$\frac{2}{x(x-1)}$=$\frac{2(x+1)}{x(x+1)(x-1)}$,
$\frac{1}{{x}^{2}-1}$=$\frac{1}{(x+1)(x-1)}$=$\frac{x}{x(x+1)(x-1)}$.
点评 本题考查通分、约分,解题的关键是明确怎么约分、在通分中会找最简公分母.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在-4,2,-1,3,-2这五个数中,最小的数是( )
| A. | -4 | B. | 2 | C. | -1 | D. | 3 |
5. 某超市在晚间优惠销售橘子,购买2千克以下按原价,购买2千克以上按优惠价.购买橘子的总价钱y(元)与购买橘子的总质量x(千克)之间的函数关系的图象如图所示,则一次性购买5千克橘子比分五次购买1千克橘子可节省( )
某超市在晚间优惠销售橘子,购买2千克以下按原价,购买2千克以上按优惠价.购买橘子的总价钱y(元)与购买橘子的总质量x(千克)之间的函数关系的图象如图所示,则一次性购买5千克橘子比分五次购买1千克橘子可节省( )
 某超市在晚间优惠销售橘子,购买2千克以下按原价,购买2千克以上按优惠价.购买橘子的总价钱y(元)与购买橘子的总质量x(千克)之间的函数关系的图象如图所示,则一次性购买5千克橘子比分五次购买1千克橘子可节省( )
某超市在晚间优惠销售橘子,购买2千克以下按原价,购买2千克以上按优惠价.购买橘子的总价钱y(元)与购买橘子的总质量x(千克)之间的函数关系的图象如图所示,则一次性购买5千克橘子比分五次购买1千克橘子可节省( )| A. | 12元 | B. | 10元 | C. | 8元 | D. | 6元 |
3.下列等式由左边至右边的变形中,属于因式分解的是( )
| A. | x2+5x-1=x(x+5)-1 | B. | x2-4+3x=+3x | C. | x2-9=(x+3)(x-3) | D. | (x+2)(x-2)=x2-4 |

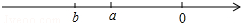 已知:表示a、b两个实数的点在数轴上的位置如图所示,化简|a-b|+$\sqrt{(a+b)^{2}}$=-2b.
已知:表示a、b两个实数的点在数轴上的位置如图所示,化简|a-b|+$\sqrt{(a+b)^{2}}$=-2b.