题目内容
10.如果要使关于x的方程$\frac{x}{x-3}$+1-3m=$\frac{m}{x-3}$有唯一解,那么m的取值范围是m≠$\frac{2}{3}$且m≠3.分析 分式方程去分母转化为整式方程,根据分式方程有唯一解得到2-2m≠0,分式有意义的条件可得3(2-2m)≠3-5m,解不等式即可得到m的取值范围.
解答 解:分式方程去分母得:x-3m(x-3)+(x-3)=m,
整理得(2-3m)x=3-8m,
由分式方程有唯一解得到2-3m≠0,即m≠$\frac{2}{3}$,
由分式有意义的条件可得3(2-3m)≠3-8m,解得m≠3.
故答案为:m≠$\frac{2}{3}$且m≠3.
点评 本题考查了分式方程的解,掌握分式有意义的条件和解不等式是解题的关键,此题难度适中.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
20.请先将下式化简,再在0,±1,±2这5个数中选择一个适当的数作为a值代入求值.
1-$\frac{a-1}{a}$÷($\frac{a}{a+2}$-$\frac{1}{{a}^{2}+2a}$)
1-$\frac{a-1}{a}$÷($\frac{a}{a+2}$-$\frac{1}{{a}^{2}+2a}$)
1.在-4,2,-1,3,-2这五个数中,最小的数是( )
| A. | -4 | B. | 2 | C. | -1 | D. | 3 |
5. 某超市在晚间优惠销售橘子,购买2千克以下按原价,购买2千克以上按优惠价.购买橘子的总价钱y(元)与购买橘子的总质量x(千克)之间的函数关系的图象如图所示,则一次性购买5千克橘子比分五次购买1千克橘子可节省( )
某超市在晚间优惠销售橘子,购买2千克以下按原价,购买2千克以上按优惠价.购买橘子的总价钱y(元)与购买橘子的总质量x(千克)之间的函数关系的图象如图所示,则一次性购买5千克橘子比分五次购买1千克橘子可节省( )
 某超市在晚间优惠销售橘子,购买2千克以下按原价,购买2千克以上按优惠价.购买橘子的总价钱y(元)与购买橘子的总质量x(千克)之间的函数关系的图象如图所示,则一次性购买5千克橘子比分五次购买1千克橘子可节省( )
某超市在晚间优惠销售橘子,购买2千克以下按原价,购买2千克以上按优惠价.购买橘子的总价钱y(元)与购买橘子的总质量x(千克)之间的函数关系的图象如图所示,则一次性购买5千克橘子比分五次购买1千克橘子可节省( )| A. | 12元 | B. | 10元 | C. | 8元 | D. | 6元 |
20.我国一次性建成最长的万吨重载铁路-晋豫鲁重载铁路,铁路全线长1260公里,横跨山西、河南、山东三省,总投资941亿元,941亿用科学记数法表示为( )
| A. | 941×108 | B. | 94.1×109 | C. | 9.41×1010 | D. | 9.41×1011 |
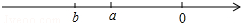 已知:表示a、b两个实数的点在数轴上的位置如图所示,化简|a-b|+$\sqrt{(a+b)^{2}}$=-2b.
已知:表示a、b两个实数的点在数轴上的位置如图所示,化简|a-b|+$\sqrt{(a+b)^{2}}$=-2b.