题目内容
10．直线y=2x+6与两坐标轴围成的三角形面积是（ ）| A． | 2 | B． | 4.5 | C． | 9 | D． | 18 |
分析 先根据直线解析式求得直线y=2x+6与坐标轴交点坐标，再计算围成的三角形面积即可．
解答 解：在直线y=2x+6中，
当x=0时，y=6；
当y=0时，x=-3；
∴直线y=2x+6与坐标轴交于（0，6），（-3，0）两点，
∴直线y=2x+6与两坐标轴围成的三角形面积=$\frac{1}{2}$×6×3=9．
故选（C）
点评 本题主要考查了一次函数图象上的点的坐标特征，解决问题的关键是利用直线解析式求直线与坐标轴的交点．注意：横轴上的点的纵坐标为0，纵轴上的点的横坐标为0．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
20．若$\sqrt{3}$=a，$\sqrt{30}$=b，则$\sqrt{0.9}$=（ ）
| A． | $\frac{a}{10b}$ | B． | $\frac{b}{10a}$ | C． | $\frac{ab}{10}$ | D． | $\frac{a+b}{10}$ |
如图所示，BE平分∠ABC，DE∥BC，观察图中相等的角共有多少对？请你把它们都写出来．（用∠x=∠y的形式写具体）
20．
某工厂投入生产一种机器，当该机器生产数量至少10台，但不超过70台，每台成本y与生产数量x之间是一次函数关系，函数y与自变量x的部分对应值如表：
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
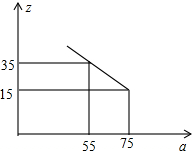
（2）市场调查发现，这种机器每月销售量z（台）与售价a（万元∕台）之间满足如图所示的函数关系，求z与a之间的函数关系式．
（3）若该厂第一个月生产这种机器50台，且第一个月按同一售价共卖出这种机器25台，请你求出该厂第一个月销售这种机器的利润．（注：利润=售价-成本）
某工厂投入生产一种机器，当该机器生产数量至少10台，但不超过70台，每台成本y与生产数量x之间是一次函数关系，函数y与自变量x的部分对应值如表：| x（单位：台） | 10 | 20 | 30 |
| y（单位：万元∕台） | 60 | 55 | 50 |
（2）市场调查发现，这种机器每月销售量z（台）与售价a（万元∕台）之间满足如图所示的函数关系，求z与a之间的函数关系式．
（3）若该厂第一个月生产这种机器50台，且第一个月按同一售价共卖出这种机器25台，请你求出该厂第一个月销售这种机器的利润．（注：利润=售价-成本）