题目内容
2.甲、乙两同学同时从400m环形跑道上的同一点出发,同向而行,甲的速度为6m/s,乙的速度为4m/s,设经过x(单位:s)后,跑道上两人的距离(较短部分)为y(单位:m),则y与x(0≤x≤300)之间的函数关系可用图象表示为( )| A. | 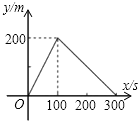 | B. | 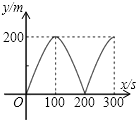 | C. | 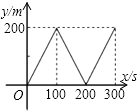 | D. | 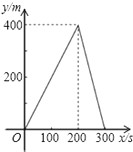 |
分析 根据同向而行,二人的速度差为6-4=2m/s,二人间的最长距离为200,最短距离为0,从而可以解答本题.
解答 解:由题意可知,
刚开始甲在乙的前面,甲在前面到甲比乙多跑一圈用的时间为:400÷(6-4)=200s,
当t=100时,二人相距(6-4)×100=200米,此时y=200,
当t=200时,二人相距(6-4)×200=400米,此时y=0,
当y=300时,二人相距(6-4)×300=600米,此时y=200,
∵y是较短部分,
∴y=$\left\{\begin{array}{l}{2x}&{(0≤x≤100)}\\{400-2x}&{(100<x≤200)}\\{2x-400}&{(200<x≤300)}\end{array}\right.$
故选C.
点评 本题考查函数的图象,解题的关键是正确理解函数图象表示的意义,明白各个过程对应的函数图象.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
10.直线y=2x+6与两坐标轴围成的三角形面积是( )
| A. | 2 | B. | 4.5 | C. | 9 | D. | 18 |
17.计算1252016×(-0.008)2015的结果为( )
| A. | -$\frac{1}{125}$ | B. | -125 | C. | $\frac{1}{125}$ | D. | 125 |
7.已知点(-1,y1)、(2,y2)、(π,y3)在双曲线y=$\frac{{k}^{2}+1}{x}$上,则下列关系式正确的是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y3>y1 | D. | y3>y1>y2 |
11.如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动.设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )


| A. | AE=6cm | B. | sin∠EBC=0.8 | ||
| C. | 当0<t≤10时,y=0.4t2 | D. | 当t=12s时,△PBQ是等腰三角形 |
 如图,在平面直角坐标系中,正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=-x2+3bx+2b+$\frac{2}{3}$经过B、C两点,则正方形OABC的周长为8.
如图,在平面直角坐标系中,正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=-x2+3bx+2b+$\frac{2}{3}$经过B、C两点,则正方形OABC的周长为8. 小刚同学把一个含有45°角的直角三角板放在如图所示的两条平行线m,n上,测得∠α=110°,则∠β的度数是65°.
小刚同学把一个含有45°角的直角三角板放在如图所示的两条平行线m,n上,测得∠α=110°,则∠β的度数是65°. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )