题目内容
8.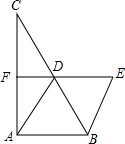 如图,△ABC中,AD是BC边的中线,分别过点B,D作AD,AB的平行线交于点E,且ED交AC于点F,AD=2DF.
如图,△ABC中,AD是BC边的中线,分别过点B,D作AD,AB的平行线交于点E,且ED交AC于点F,AD=2DF.(1)求证:四边形ABED为菱形;
(2)若BD=6,∠E=60°,求四边形ABED的面积.
分析 (1)先证明四边形ABED是平行四边形,利用三角形中位线定理可以证明AD=AB即可.
(2)求出菱形的对角线即可求面积.
解答 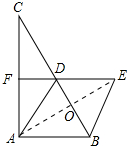 (1)证明:∵AD是BC边中线,
(1)证明:∵AD是BC边中线,
∴DC=DB,DF∥AB,
∴CF=FA,
∴AB=2DF,
∵AD=2DF,
∴AB=AD,
∵AD∥BE,DE∥AB,
∴四边形ABED是平行四边形,∵AD=AB,
∴四边形ABED是菱形.
(2)连接AE交BD于O,∵∠DEB=60°,四边形ABED是菱形,
∴△BDE、△ABD是等边三角形,DO=BO=3,
在RT△DOE中,∵DO=3,∠EDO=60°,DE=6,
∴EO=$\sqrt{D{E}^{2}-D{O}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴AE=2EO=6$\sqrt{3}$,
∴S菱形ABED=$\frac{1}{2}$•AE•BD=$\frac{1}{2}$×6$\sqrt{3}$×6=18$\sqrt{3}$.
点评 本题考查菱形的判定和性质、三角形中位线定理、菱形的面积公式,记住菱形的面积等于对角线乘积的一半,属于中考常考题型.

练习册系列答案
相关题目
13.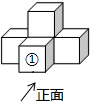 如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
 如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )| A. | 主视图与左视图不变 | B. | 左视图与俯视图不变 | ||
| C. | 主视图与俯视图改变 | D. | 左视图与俯视图改变 |
20.下列由左到右的变形中属于因式分解的是( )
| A. | 24x2y=3x•8xy | B. | m2-2m-3=m(m-2)-3 | C. | x2+2x+1=(x+1)2 | D. | (x+3)(x-3)=x2-9 |
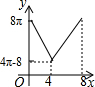
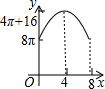
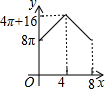
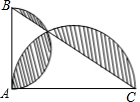 如图,△ABC中,∠BAC=90°,AC+AB=8,以AC、AB为半径作半圆.记图中阴影部分面积为y,AC为x,则下列y关于x的图象正确的是( )
如图,△ABC中,∠BAC=90°,AC+AB=8,以AC、AB为半径作半圆.记图中阴影部分面积为y,AC为x,则下列y关于x的图象正确的是( )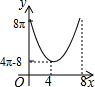
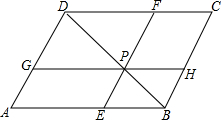 如图,在?ABCD中,P是对角线BD上的一点,过P点的直线EF∥BC.GH∥AB.则图中面积相等的四边形有5对.
如图,在?ABCD中,P是对角线BD上的一点,过P点的直线EF∥BC.GH∥AB.则图中面积相等的四边形有5对.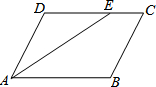 如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.
如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.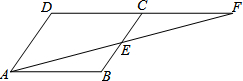 如图,?ABCD中,E是BC的中点,连结AE并延长交DC的延长线于F.试问:AB与CF相等吗?请说明理由.
如图,?ABCD中,E是BC的中点,连结AE并延长交DC的延长线于F.试问:AB与CF相等吗?请说明理由.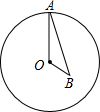 如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.
如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.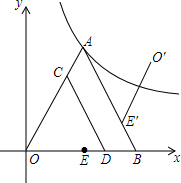 如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.
如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.