题目内容
6．
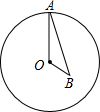如图，点A为⊙O上一个动点，点B在⊙O内，且OA=2$\sqrt{3}$，OB=2，当∠OAB的度数取最大值时，AB的长度为2$\sqrt{2}$．
分析 当AB⊥OB时，∠OBA取得最大值，然后在直角△OBA中利用勾股定理求AB的值即可．
解答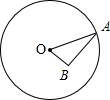 
解：∵AB⊥OB时，∠OAB的度数最大，
∴Rt△OBA中，OA=2$\sqrt{3}$，OB=2，
∴AB=$\sqrt{O{A}^{2}-O{B}^{2}}$=$\sqrt{（2{\sqrt{3}）}^{2}-{2}^{2}}$=2$\sqrt{2}$；
故答案为：2$\sqrt{2}$．
点评 本题考查了勾股定理．解答此题的关键是找出“当AB⊥OB时，∠OBA取最大值”这个隐含条件．
练习册系列答案
相关题目
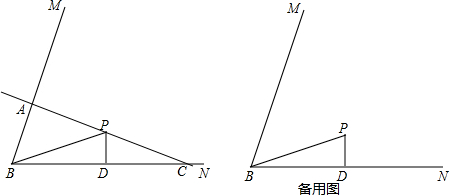
在平行四边形ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF=BE，连接AF，BF．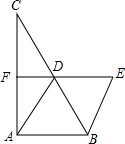
如图，△ABC中，AD是BC边的中线，分别过点B，D作AD，AB的平行线交于点E，且ED交AC于点F，AD=2DF．
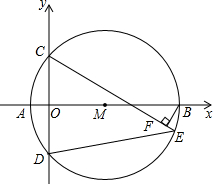已知关于x的方程x2+（2m-6）x+m2-7=0有两个不相等的实数根，两根的平方和为10，且两根分别是A点和B点的横坐标（如图），以AB为直径作圆M交y轴于点C和点D，点E是$\widehat{BD}$上一点，BF⊥CE于点F，连接DE．
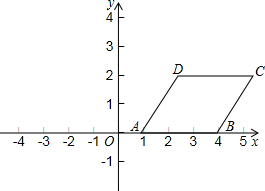如图，在平面直角坐标系中．?ABCD四个顶点的坐标分别为A（1，0），B（4，0），C（5，2），D（2，2）．请你按下列要求画出?ABCD变换后的图形，并写出变换后的图形四个顶点的坐标．