题目内容
7.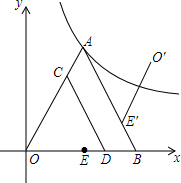 如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.
如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.(1)当点E′落在AB上时,x的值为4.5
(2)当O′E′与反比例函数图象有交点时,x的取值范围是2$\sqrt{3}$≤x≤6.
分析 (1)连接AE,设OE=a,根据等边三角形的性质,轴对称的性质以及平行线的性质得出D是EB的中点,进而得出x的值;
(2)根据题意,O′E′在过D点平行于OA的直线上,当O′落在反比例函数图象上时,根据对称的性质O′D=OD=OC=x,得出O′坐标,当O′落在反比例函数图象上时,列出关于x的方程,从而求得x的取值范围.
解答 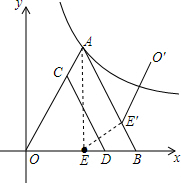 解:(1)连接AE,
解:(1)连接AE,
∵△AOB是等边三角形,点E是OB的中点,
∴AE⊥OB,
设OE=a,则AE=$\sqrt{3}$a,
∴A(a,$\sqrt{3}$a),
∴a•$\sqrt{3}$a=9$\sqrt{3}$,
解得a=3,
∴OE=EB=3,
∴OA=OB=6,
连接EE′,
∵E和E′关于直线CD对称,
∴EE′⊥CD,
∴AB∥CD,
∴EE′⊥AB,
∵点E′落在AB上,
∴CD⊥EE′且平分EE′,
∴D是EB的中点,
∴OD=4.5,
∴OC=OD=4.5,
∴x=4.5.
(2)根据题意,O′E′在过D点平行于OA的直线上,根据对称的性质O′D=OD=OC=x,
∴O′($\frac{3}{2}$x,$\frac{\sqrt{3}}{2}$x),
当O′落在反比例函数图象上时,
则$\frac{3}{2}$x•$\frac{\sqrt{3}}{2}$x=9$\sqrt{3}$,
解得x=2$\sqrt{3}$,
∵C为边OA上一点,OA=6,
∴O′E′与反比例函数图象有交点时,x的取值范围是2$\sqrt{3}$≤x≤6.
故答案为4.5;2$\sqrt{3}$≤x≤6.
点评 本题考查了反比例函数和一次函数的交点问题,涉及的知识有:等边三角形的性质,轴对称的性质,解直角三角形等,熟练掌握轴对称的性质是解本题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
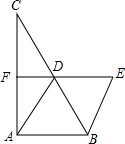 如图,△ABC中,AD是BC边的中线,分别过点B,D作AD,AB的平行线交于点E,且ED交AC于点F,AD=2DF.
如图,△ABC中,AD是BC边的中线,分别过点B,D作AD,AB的平行线交于点E,且ED交AC于点F,AD=2DF.
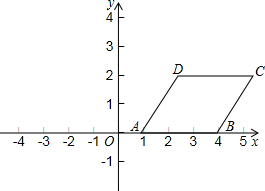 如图,在平面直角坐标系中.?ABCD四个顶点的坐标分别为A(1,0),B(4,0),C(5,2),D(2,2).请你按下列要求画出?ABCD变换后的图形,并写出变换后的图形四个顶点的坐标.
如图,在平面直角坐标系中.?ABCD四个顶点的坐标分别为A(1,0),B(4,0),C(5,2),D(2,2).请你按下列要求画出?ABCD变换后的图形,并写出变换后的图形四个顶点的坐标.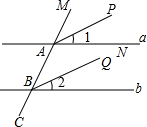 如图,已知AP和BQ分别平分∠MAN和∠ABR,且∠1=∠2,求证:a∥b.
如图,已知AP和BQ分别平分∠MAN和∠ABR,且∠1=∠2,求证:a∥b.