题目内容
18.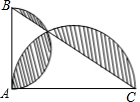 如图,△ABC中,∠BAC=90°,AC+AB=8,以AC、AB为半径作半圆.记图中阴影部分面积为y,AC为x,则下列y关于x的图象正确的是( )
如图,△ABC中,∠BAC=90°,AC+AB=8,以AC、AB为半径作半圆.记图中阴影部分面积为y,AC为x,则下列y关于x的图象正确的是( )| A. | 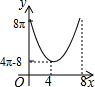 | B. | 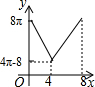 | C. | 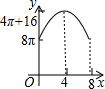 | D. | 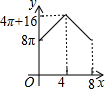 |
分析 根据题意和图象,可知阴影部分的面积等于以AB和AC为直径的半圆的面积之和与直角三角形ABC的面积之差,从而可以表示出阴影部分的面积,从而可以得到y关于x的函数图象,本题得以解决.
解答 解:由图可知,
阴影部分的面积是:y=$\frac{1}{2}π•(\frac{x}{2})^{2}+\frac{1}{2}π•(\frac{8-x}{2})^{2}-\frac{x(8-x)}{2}$=$(\frac{π}{4}+\frac{1}{2}){x}^{2}-(2π+4)x+8π$,
∵$\frac{π}{4}+\frac{1}{2}>0$,
∴y关于x的解析式是抛物线,开口向上,有最小值.
故选A.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,可以表示出阴影部分的面积.

练习册系列答案
相关题目
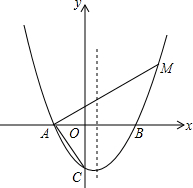 已知抛物线y=$\frac{1}{a}{x}^{2}+(\frac{2}{a}-1)x-2$(a>0)与x轴交于A、B,与y轴相交于点C,且点A在点B的左侧.
已知抛物线y=$\frac{1}{a}{x}^{2}+(\frac{2}{a}-1)x-2$(a>0)与x轴交于A、B,与y轴相交于点C,且点A在点B的左侧.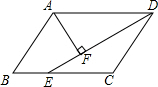 如图,?ABCD中,DE平分∠ADC交BC于E,AF⊥DE于F,已知∠DAF=58°,则∠B=64°.
如图,?ABCD中,DE平分∠ADC交BC于E,AF⊥DE于F,已知∠DAF=58°,则∠B=64°. 在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.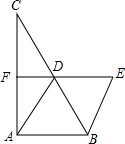 如图,△ABC中,AD是BC边的中线,分别过点B,D作AD,AB的平行线交于点E,且ED交AC于点F,AD=2DF.
如图,△ABC中,AD是BC边的中线,分别过点B,D作AD,AB的平行线交于点E,且ED交AC于点F,AD=2DF.