题目内容
11．已知方程x2+mx+n=0的两根为x1、x2（x1＜x2），方程x2+mx+n-1=0的两根为x3、x4（x3＜x4），则下列关系一定成立的是（ ）| A． | x1＜x2＜x3＜x4 | B． | x1＜x3＜x4＜x2 | C． | x3＜x4＜x1＜x2 | D． | x3＜x1＜x2＜x4 |
分析 先利用根与系数的关系得出x1+x2=x3+x4=-m，x1x2=n＞x3x4=n-1，再根据如果两个数的和一定，那么它们的差越大积越小即可得到x3＜x1＜x2＜x4．
解答 解：∵方程x2+mx+n=0的两根为x1、x2（x1＜x2），
∴x1+x2=-m，x1x2=n，
∵方程x2+mx+n-1=0的两根为x3、x4（x3＜x4），
∴x3+x4=-m，x3x4=n-1，
∴x1+x2=x3+x4=-m，x1x2=n＞x3x4=n-1，
∴x3＜x1＜x2＜x4．
故选D．
点评 本题考查了根与系数的关系：x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．本题还可以利用求根公式分别求出x1、x2、x3、x4的值，再比较大小．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
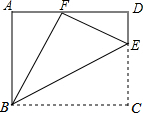如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上．若sin∠DFE=$\frac{1}{3}$，则 tan∠EBC的值为$\frac{\sqrt{2}}{2}$．
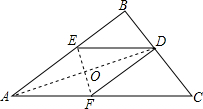如图，在三角形纸片ABC中，∠BAC为锐角，AB=12cm，AC=15cm．按下列步骤折叠：第一次，把∠B折叠使点B落在AC边上，折痕为AD，交BC于点D；第二次折叠，使点A与点D重合，折痕分别交AB、AC于点E、F，EF与AD交于点O，展开后，连结DE、DF．
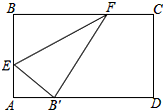如图，折叠矩形纸片ABCD，使点B落在边AD上，折痕EF的两端分别在AB、BC上（含端点），且AB=6cm，BC=10cm．求折痕EF的最大值．
3．
如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（ ）
如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（ ）| A． | 70° | B． | 50° | C． | 40° | D． | 80° |