题目内容
4.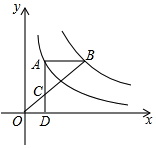 如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
分析 过点B作BE⊥x轴于E,延长线段BA,交y轴于F,得出四边形AFOD是矩形,四边形OEBF是矩形,得出S矩形AFOD=4,S矩形OEBF=k,根据平行线分线段成比例定理证得AB=2OD,即OE=3OD,即可求得矩形OEBF的面积,根据反比例函数系数k的几何意义即可求得k的值.
解答  解:过点B作BE⊥x轴于E,延长线段BA,交y轴于F,
解:过点B作BE⊥x轴于E,延长线段BA,交y轴于F,
∵AB∥x轴,
∴AF⊥y轴,
∴四边形AFOD是矩形,四边形OEBF是矩形,
∴AF=OD,BF=OE,
∴AB=DE,
∵点A在双曲线y=$\frac{4}{x}$上,
∴S矩形AFOD=4,
同理S矩形OEBF=k,
∵AB∥OD,
∴$\frac{OD}{AB}$=$\frac{CD}{AC}$=$\frac{1}{2}$,
∴AB=2OD,
∴DE=2OD,
∴S矩形OEBF=3S矩形AFOD=12,
∴k=12.
故选D.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
14.根据函数y=$\frac{1}{x}$的图象,判断当x≥-1时,y的取值范围是( )
| A. | y<-1 | B. | y≤-1 | C. | y≤-1或y>0 | D. | y<-1或y≥0 |
15.从分别标有数-3,-2,-1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不是正数的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
12.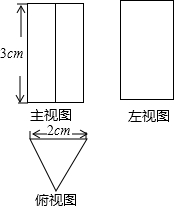 如图是一个几何体的三视图,则这个几何体的体积是( )
如图是一个几何体的三视图,则这个几何体的体积是( )
 如图是一个几何体的三视图,则这个几何体的体积是( )
如图是一个几何体的三视图,则这个几何体的体积是( )| A. | 3$\sqrt{3}$cm3 | B. | 6$\sqrt{3}$cm3 | C. | 6cm3 | D. | 12cm3 |
9.在3,0,π,-4这四个数中,最大的是( )
| A. | 3 | B. | 0 | C. | π | D. | -4 |
16.某种商品一周内卖出的件数从周一到周日统计如下:26,36,22,22,24,31,21,关于这组数据,下列说法错误的是( )
| A. | 方差是21 | B. | 平均数是26 | C. | 众数是22 | D. | 中位数是24 |
13.下列运算正确的是( )
| A. | 8a2-4a=4a | B. | (-a3b)2=a6b2 | C. | a-2+a2=a0 | D. | a2•4a4=4a8 |
14.某创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表:
现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中正确的有( )
①平均日工资增大 ②日工资的方差减小
②日工资的中位数不变 ④日工资的众数不变.
| 研发组 | 管理组 | 操作组 | |
| 日工资(元) | 200 | 180 | 160 |
| 人数(人) | 3 | 4 | 5 |
①平均日工资增大 ②日工资的方差减小
②日工资的中位数不变 ④日工资的众数不变.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |