题目内容
12．
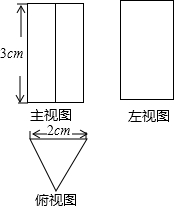如图是一个几何体的三视图，则这个几何体的体积是（ ）| A． | 3$\sqrt{3}$cm3 | B． | 6$\sqrt{3}$cm3 | C． | 6cm3 | D． | 12cm3 |
分析 首先确定该几何体的形状，然后利用底面积乘以高球的体积即可．
解答 解：观察该几何体的三视图，发现该几何体为正三棱柱，
其地面边长为2，高为3，
所以其体积为$\frac{1}{2}$×2×$\sqrt{3}$×3=3$\sqrt{3}$cm3，
故选A．
点评 本题考查了由三视图判断几何体的知识，解题的关键是根据三视图判断该几何体的形状，难度不大．
练习册系列答案
期末集结号系列答案
相关题目
2．|-2017|的相反数是（ ）
| A． | 2017 | B． | $\frac{1}{2017}$ | C． | -2017 | D． | -$\frac{1}{2017}$ |
3．肥皂泡的泡壁厚度大约是0.0000007m，用科学记数法可表示为（ ）m．
| A． | 0.7×10-6 | B． | 0.7×10-7 | C． | 7×10-6 | D． | 7×10-7 |
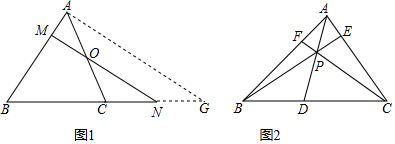
20．
如图，点A在以BC为直径的⊙O内，且AB=AC，以点A为圆心，AC长为半径作弧，得到扇形ABC，剪下扇形ABC围成一个圆锥（AB和AC重合），若∠BAC=120°，BC=4$\sqrt{3}$，则圆锥底面圆的半径是（ ）
如图，点A在以BC为直径的⊙O内，且AB=AC，以点A为圆心，AC长为半径作弧，得到扇形ABC，剪下扇形ABC围成一个圆锥（AB和AC重合），若∠BAC=120°，BC=4$\sqrt{3}$，则圆锥底面圆的半径是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{2}{3}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
7．已知⊙O是△ABC的外接圆，边BC=4cm，且⊙O半径也为4cm，则∠A的度数是（ ）
| A． | 30° | B． | 60°或120° | C． | 150° | D． | 30°或150° |
17．已知正比例函数y=3x，若该正比例函数经过点（m，6m-1），则m的值为（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | $\frac{1}{2}$ |
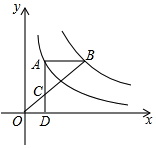如图，点A在双曲线y=$\frac{4}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，过点A作AD⊥x轴于D．连接OB，与AD相交于点C，若AC=2CD，则k的值为（ ）
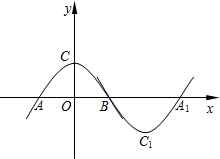如图所示，抛物线l1：y=ax2+b（a＜0，b＞0）与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，将抛物线l1绕点B旋转180°，得到新的抛物线l2，它的顶点为C1，与x轴的另一个交点为A1