题目内容
14.某创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表:| 研发组 | 管理组 | 操作组 | |
| 日工资(元) | 200 | 180 | 160 |
| 人数(人) | 3 | 4 | 5 |
①平均日工资增大 ②日工资的方差减小
②日工资的中位数不变 ④日工资的众数不变.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据平均数、方差、中位数和众数的定义分别对每一项进行分析,即可得出答案.
解答 解:调整前的平均数是$\frac{200×3+180×4+160×5}{3+4+5}$=$\frac{530}{3}$,
调整后的平均数是$\frac{200×4+180×2+160×6}{4+2+6}$=$\frac{530}{6}$,
则团队平均日工资不变,
故①错误;
调整前的方差是$\frac{1}{12}$[3(200-$\frac{530}{3}$)2+4(180-$\frac{530}{3}$)2+5(160-$\frac{530}{3}$)2]=$\frac{9200}{3}$,
调整后的方差是$\frac{1}{12}$[4(200-$\frac{530}{3}$)2+2(180-$\frac{530}{3}$)2+6(160-$\frac{530}{3}$)2]=$\frac{11600}{3}$,
则日工资的方差变大,
故②错误;
调整前:把这些数从小到大排列为:200,200,200,180,180,180,180,160,160,160,160,160,
最中间两个数的平均数是:$\frac{180+180}{2}$=180,
则中位数是280,
调整后:把这些数从小到大排列为:把这些数从小到大排列为:200,200,200,200,180,180,160,160,160,160,160,160,
最中间两个数的平均数是:$\frac{180+160}{2}$=170,
则中位数是170,
曰工资的中位数变小,
故③错误;
调整前的众数是160,调整后的众数也是160,则众数不变,
故④正确;
故选A.
点评 此题考查了平均数、方差、中位数和众数,用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数;方差公式是S2=S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].

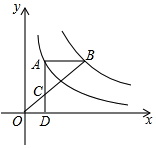 如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
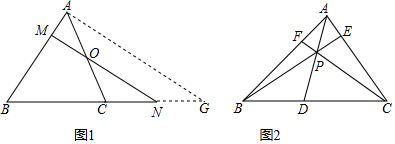
 如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,(1)点点同学通过画图和测量得到以下近似数据:
| ɑ | 30° | 40° | 50° | 60° |
| β | 120° | 130° | 140° | 150° |
| γ | 150° | 140° | 130° | 120° |
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
| A. | 20% | B. | 25% | C. | 50% | D. | 62.5% |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
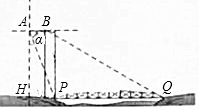 如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的 ;
;