题目内容
15.从分别标有数-3,-2,-1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不是正数的概率是( )| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
分析 让卡片上的数的绝对值不是正数的卡片数除以总卡片数即为所求的概率,即可选出.
解答 解:∵七张卡片分别标有-3,-2,-1,0,1,2,3七个数,数的绝对值不是正数的卡片有1张,
∴从中随机抽取一张卡片数的绝对值不是正数的概率为$\frac{1}{7}$.
故选A.
点评 本题考查随机事件概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
5.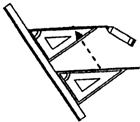 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )| A. | 两直线平行,同位角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 同位角相等,两直线平行 | D. | 内错角相等,两直线平行 |
6.若二次根式$\sqrt{2x-6}$在实数范围内有意义,则x的取值范围是( )
| A. | x≤3 | B. | x>3 | C. | x≥3 | D. | x>-3 |
3.肥皂泡的泡壁厚度大约是0.0000007m,用科学记数法可表示为( )m.
| A. | 0.7×10-6 | B. | 0.7×10-7 | C. | 7×10-6 | D. | 7×10-7 |
20. 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
7.已知⊙O是△ABC的外接圆,边BC=4cm,且⊙O半径也为4cm,则∠A的度数是( )
| A. | 30° | B. | 60°或120° | C. | 150° | D. | 30°或150° |
4.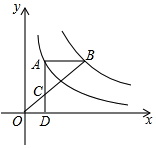 如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
 如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
5. 如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
 如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,(1)点点同学通过画图和测量得到以下近似数据:
| ɑ | 30° | 40° | 50° | 60° |
| β | 120° | 130° | 140° | 150° |
| γ | 150° | 140° | 130° | 120° |
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.