题目内容
9.在3,0,π,-4这四个数中,最大的是( )| A. | 3 | B. | 0 | C. | π | D. | -4 |
分析 正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可.
解答 解:根据实数比较大小的方法,可得:-4<0<3<π,
∴在3,0,π,-4这四个数中,最大的是π,
故选:C.
点评 此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.分解因式:x2y-4y结果正确的是( )
| A. | y(x2-4) | B. | y(x-2)2 | C. | y(x+2)2 | D. | y(x+2)(x-2) |
20. 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
17.已知正比例函数y=3x,若该正比例函数经过点(m,6m-1),则m的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{2}$ |
4.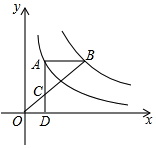 如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
 如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{4}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
18.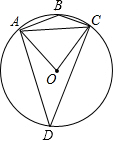 如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )
如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )
 如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )
如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )| A. | 30° | B. | 50° | C. | 40° | D. | 45° |
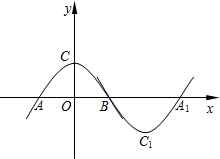 如图所示,抛物线l1:y=ax2+b(a<0,b>0)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,将抛物线l1绕点B旋转180°,得到新的抛物线l2,它的顶点为C1,与x轴的另一个交点为A1
如图所示,抛物线l1:y=ax2+b(a<0,b>0)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,将抛物线l1绕点B旋转180°,得到新的抛物线l2,它的顶点为C1,与x轴的另一个交点为A1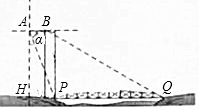 如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的