题目内容
5.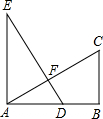 如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )
如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )①DE=AC;②DE⊥AC;③∠EAF=∠ADE;④∠CAB=30°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据点D是AB的中点,得到AD=$\frac{AB}{2}$,由于AB=2BC,于是得到AD=BC,证得Rt△AED≌Rt△BAC,得到∠E=∠CAB,DE=AC,故①正确;由∠E+∠EDA=90°,得到∠FAD+∠EDA=90°,即可得到DE⊥AC,故②正确;根据同角的余角相等得到∠EAF=∠ADE,故③正确;根据BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,故④错误.
解答 解:点D是AB的中点,则AD=$\frac{AB}{2}$,
∵AB=2BC ,
,
∴AD=BC,
∵EA⊥AB,CB⊥AB,
∴∠B=∠EAB=90°,
在△AED与△BAC中,
$\left\{\begin{array}{l}{AD=BC}\\{∠DAE=∠CBA}\\{AE=AB}\end{array}\right.$,
∴△AED≌△BAC,
∴∠E=∠CAB,DE=AC,
∴①正确;
∵∠E+∠EDA=90°,
∴∠FAD+∠EDA=90°,
∴∠AFD=180°-(∠FAD+∠EDA)=90°,
∴DE⊥AC,
∴②正确;
∵∠EAF与∠ADE都是∠E的余角,
∴∠EAF=∠ADE,
∴③正确;
∵BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,
∴④错误;
故选C.
点评 本题考查了:①全等三角形的判定和性质;②三角形内角和定理;③直角三角形的性质,熟记这些定理是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
13. 如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
 如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
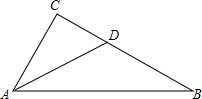 如图,△ABC中,∠C=90°,∠BAC=60°,AD是角平分线,若BD=6,则CD等于( )
如图,△ABC中,∠C=90°,∠BAC=60°,AD是角平分线,若BD=6,则CD等于( )
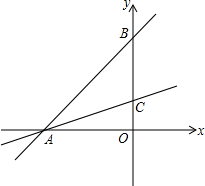 如图,直线y=x+1与x轴、y轴分别相交于点A、B,过点A的直线y=$\frac{1}{3}$x+b与y轴相交于点C.
如图,直线y=x+1与x轴、y轴分别相交于点A、B,过点A的直线y=$\frac{1}{3}$x+b与y轴相交于点C.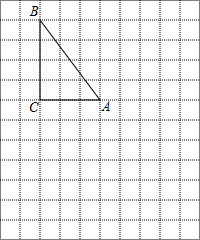 在下列网格中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4,
在下列网格中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4,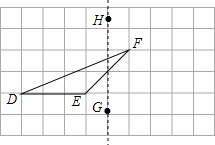 如图,在正方形网格上有一个△DEF.
如图,在正方形网格上有一个△DEF.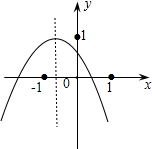 小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )
小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )