题目内容
10.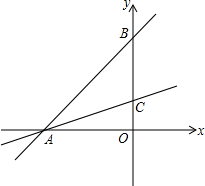 如图,直线y=x+1与x轴、y轴分别相交于点A、B,过点A的直线y=$\frac{1}{3}$x+b与y轴相交于点C.
如图,直线y=x+1与x轴、y轴分别相交于点A、B,过点A的直线y=$\frac{1}{3}$x+b与y轴相交于点C.(1)求直线AC的解析式;
(2)求直线AC关于直线AB对称的直线的解析式.
分析 (1)由直线y=x+1求得A的坐标,代入直线y=$\frac{1}{3}$x+b,根据待定系数法即可求得;
(2)根据待定系数法求得直线CC′的解析式,联立方程求得D的坐标,即可求得对称点C′的坐标,然后利用待定系数法求得即可.
解答  解:(1)∵直线y=x+1与x轴、y轴分别相交于点A、B,
解:(1)∵直线y=x+1与x轴、y轴分别相交于点A、B,
∴B(0,1),A(-1,0),
∵直线y=$\frac{1}{3}$x+b过A点,
∴0=-$\frac{1}{3}$+b,
解得:b=$\frac{1}{3}$,
∴C(0,$\frac{1}{3}$),
设AC解析式为y=kx+a,
∵过A(-1,0),C(0,$\frac{1}{3}$),
∴$\left\{\begin{array}{l}{0=-k+a}\\{a=\frac{1}{3}}\end{array}\right.$,
解得:k=$\frac{1}{3}$,a=$\frac{1}{3}$,
∴AC解析式为y=$\frac{1}{3}$x+$\frac{1}{3}$;
(2)作C关于直线AB的对称点C′,连接CC′交AB于D,则AD⊥CC′,
∴直线CC′的解析式为y=-x+$\frac{1}{3}$,
解$\left\{\begin{array}{l}{y=x+1}\\{y=-x+\frac{1}{3}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{1}{3}}\\{y=\frac{2}{3}}\end{array}\right.$,
∴D(-$\frac{1}{3}$,$\frac{2}{3}$),
设C′(x,y),
∵-$\frac{1}{3}$=$\frac{x+0}{2}$,$\frac{2}{3}$=$\frac{y+\frac{1}{3}}{2}$,
∴x=-$\frac{2}{3}$,y=1,
∴C′(-$\frac{2}{3}$,1),
设直线AC′的解析式为y=mx+n,
∵A(-1,0),
∴$\left\{\begin{array}{l}{-m+n=0}\\{-\frac{2}{3}m+n=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=3}\\{n=3}\end{array}\right.$,
∴直线AC关于直线AB对称的直线的解析式为y=3x+3.
点评 本题考查了待定系数法求一次函数的解析式,轴对称的性质,互相垂直两直线的性质等,熟练掌握待定系数法是解题的关键.

| A. | x3•x2=x6 | B. | 3x2-2x2=x2 | C. | (x2)3=x5 | D. | $\sqrt{4}$=±2 |
 如图,在梯形ABCD中,AD∥BC,已知AD=2,BD=6,AC=BC=8,求证:AC⊥BD.
如图,在梯形ABCD中,AD∥BC,已知AD=2,BD=6,AC=BC=8,求证:AC⊥BD.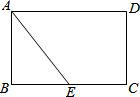 如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是$\frac{18}{5}$ cm.
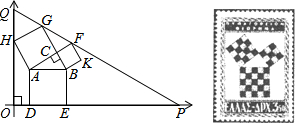
如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是$\frac{18}{5}$ cm.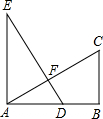 如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )
如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )
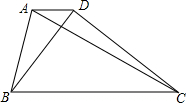
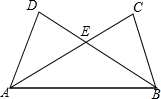 已知,如图,AD=BC,AC=BD,AC与BD相交于点E.
已知,如图,AD=BC,AC=BD,AC与BD相交于点E.