题目内容
14.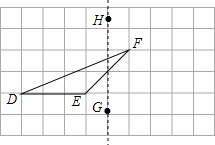 如图,在正方形网格上有一个△DEF.
如图,在正方形网格上有一个△DEF.(1)作△DEF关于直线HG的轴对称图形△ABC(不写作法);
(2)作EF边上的高(不写作法);
(3)若网格上的最小正方形边长为1,求△DEF的面积.
分析 (1)分别作出点D、E、F关于直线HG对称的点,然后顺次连接;
(2)过点D作DM垂直于直线FE的延长线于点M,然后连接DM;
(3)根据三角形的面积公式$\frac{1}{2}$×底×高即可求解.
解答 解:(1)所作图形如图所示:
△ABC即为所作图形;
(2)所作图形如图所示:
DM即为EF边上的高;
(3)S△DEF=$\frac{1}{2}$×3×2=3.
点评 本题考查了根据轴对称变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
6.在画二次函数的图象时列出了下表:
观察表格,可以得到许多信息:
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-12;
(3)函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上有三点:A(m,y1)、B(m+1,y2)、C(m+2,y3).通过计算说明:(y3-y2)与(y2-y1)的差为定值.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 0 | 3 | 4 | 3 | 0 | -5 | … |
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-12;
(3)函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上有三点:A(m,y1)、B(m+1,y2)、C(m+2,y3).通过计算说明:(y3-y2)与(y2-y1)的差为定值.
4.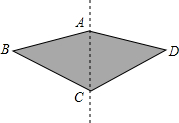 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
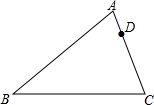 如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,且AD=4,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,请在图中画出所有符合要求的直线l,并写出所作三角形与△ABC的相似比.
如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,且AD=4,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,请在图中画出所有符合要求的直线l,并写出所作三角形与△ABC的相似比.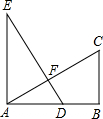 如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )
如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )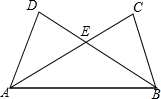 已知,如图,AD=BC,AC=BD,AC与BD相交于点E.
已知,如图,AD=BC,AC=BD,AC与BD相交于点E. 如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.