题目内容
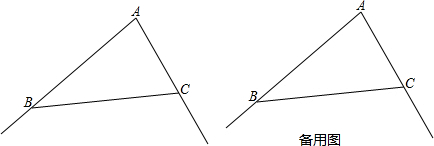
20.如图,已知△ABC(AB>AC),在∠BAC内部的点P到∠BAC两边的距离相等,且PB=PC.(1)利用尺规作图,确定符合条件的P点(保留作图痕迹,不必写出作法);
(2)过点P作AC的垂线,垂足D在AC延长线上,求证:AB-AC=2CD;
(3)当∠BAC=90°时,判断△PBC的形状,并证明你的结论;
(4)当∠BAC=90°时,设BP=m,AP=n,直接写出△ABC的周长和面积(用含m、n的代数式表示).
分析 (1)作∠BAC的平分线和线段BC的垂直平分线,两线交于点P,则点P即为所求;
(2)如图2,作PE⊥AB于点E,联结PB、PC,由点P在∠BAC的平分线上,得到PD=PE,证得Rt△PEB≌Rt△PDC,得到BE=CD,推出Rt△AEP≌Rt△ADP,得到AE=AD,由于AE=AB-BE,AD=AC+CD,即可得到结论;
(3)根据等腰直角三角形的判定和性质即可得到结论;
(4)由(3)证得△BPC是等腰直角三角形,推出△AEP是等腰直角三角形,求得AE=$\frac{\sqrt{2}}{2}$AP,即AE=$\frac{\sqrt{2}}{2}$n,由于AE=AD,BE=CD,于是得到AB+AC=AE+AD=$\sqrt{2}$n,求得△ABC的周长=$\sqrt{2}$(m+n),根据Rt△PEB≌Rt△PDC,得到S△ABC=S四边形ABPC-S△BPC=$\frac{1}{2}$n2=$\frac{1}{2}$m2.
解答 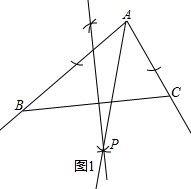 解:(1)如图1所示,点P即为所求作的点;
解:(1)如图1所示,点P即为所求作的点;
(2)如图2,作PE⊥AB于点E,联结PB、PC,
∵点P在∠BAC的平分线上,
∴PD=PE,
在Rt△PEB和Rt△PDC中,
$\left\{{\begin{array}{l}{PE=PD}\\{PB=PC}\end{array}}\right.$,
∴Rt△PEB≌Rt△PDC,
∴BE=CD,
在Rt△AEP和Rt△ADP中,
$\left\{{\begin{array}{l}{PE=PD}\\{AP=AP}\end{array}}\right.$,
∴Rt△AEP≌Rt△ADP,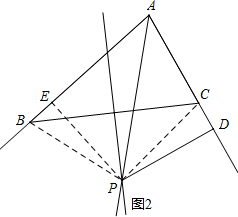
∴AE=AD,
∵AE=AB-BE,AD=AC+CD,
∴AB-BE=AC+CD,
又∵BE=CD,
∴AB-AC=2CD;
(3)∵∠BAC=90°,
∴∠EAP=∠PAC=45°,
在Rt△AEP中,∠EAP+∠EPA=90°,
∴∠EPA=45°,
同理∠APD=45°,
∴∠EPD=90°=∠EPC+∠CPD,
由(2)知Rt△PEB≌Rt△PDC,
∴∠BPE=∠CPD,
∴∠BPE+∠EPC=90°,即∠BPC=90°,
又∵BP=PC,
∴△BPC是等腰直角三角形;
(4)由(3)证得△BPC是等腰直角三角形,
∴BC=$\sqrt{2}$PB,
∵PB=m,
∴BC=$\sqrt{2}$m,
∵AP平分∠BAC,∠CAB=90°,
∴∠EAP=45°,
∴△AEP是等腰直角三角形,
∴AE=$\frac{\sqrt{2}}{2}$AP,
∵AP=n,
∴AE=$\frac{\sqrt{2}}{2}$n,
∵AE=AD,BE=CD,
∴AB+AC=AE+AD=$\sqrt{2}$n,
∴△ABC的周长=$\sqrt{2}$(m+n),
∵Rt△PEB≌Rt△PDC,
∴S四边形ABPC=S四边形AEPD=AE2=$\frac{1}{2}$n2,
∵S△ABC=S四边形ABPC-S△BPC=$\frac{1}{2}$n2=$\frac{1}{2}$m2.
点评 本题考查了全等三角形的判定和性质,正方形的性质,等腰直角三角形的判定和性质,角平分线的性质,线段垂直平分线的性质,基本作图,正确的作出辅助线是解题的关键.

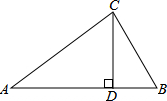 如图,CD是Rt△ABC斜边AB上的高,CD=6,BD=4,则AB的长为( )
如图,CD是Rt△ABC斜边AB上的高,CD=6,BD=4,则AB的长为( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
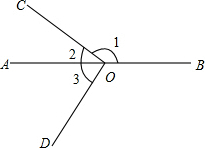 如图,已知点O在直线AB上,CO⊥DO,若∠1=155°,则∠3的度数为( )
如图,已知点O在直线AB上,CO⊥DO,若∠1=155°,则∠3的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
 如图,?ABCD的对角线AC,BD相交于点O,且AB=5,AO=4,BO=3,求证:?ABCD是菱形.
如图,?ABCD的对角线AC,BD相交于点O,且AB=5,AO=4,BO=3,求证:?ABCD是菱形.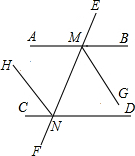 如图,已知AB∥CD,MG、NH分别平分∠BMN与∠CNM,试说明NH∥MG.
如图,已知AB∥CD,MG、NH分别平分∠BMN与∠CNM,试说明NH∥MG.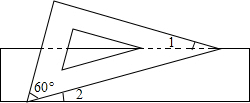 如图,有一块含有60°角的直角三角板的两个顶点放在长方形的对边上.如果∠1=16°,那么∠2的度数是14°.
如图,有一块含有60°角的直角三角板的两个顶点放在长方形的对边上.如果∠1=16°,那么∠2的度数是14°.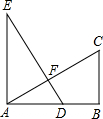 如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )
如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )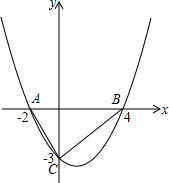 如图,二次函数的图象经过A、B、C三点
如图,二次函数的图象经过A、B、C三点