题目内容
17.用指定的方法解下列方程组:(1)$\left\{\begin{array}{l}{3x+4y=19}\\{x-y=4}\end{array}\right.$(代入法)
(2)$\left\{\begin{array}{l}{8y+5x=2}\\{4y-3x=-10}\end{array}\right.$(加减法)
(3)$\left\{\begin{array}{l}{x+2y=9}\\{3x-2y=-1}\end{array}\right.$
(4)$\left\{\begin{array}{l}{\frac{x}{4}+\frac{y}{3}=3}\\{3x-2(y-1)=11}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
(3)方程组利用加减消元法求出解即可;
(4)先把方程组中的方程化为不含分母及括号的方程,再用加减消元法求解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+4y=19①}\\{x-y=4②}\end{array}\right.$,
由②得:x=y+4,
代入①得:3y+12+4y=19,即y=1,
将y=1代入②得:x=5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{8y+5x=2①}\\{4y-3x=-10②}\end{array}\right.$,
①-②×2得:11x=22,即x=2,
将x=2代入①得:8y=-8,解得y=-1
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
(3)$\left\{\begin{array}{l}{x+2y=9①}\\{3x-2y=-1②}\end{array}\right.$
①+②得:4x=8,即x=2,
将x=2代入①得:2y=7,解得y=$\frac{7}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=\frac{7}{2}}\end{array}\right.$.
(4))原方程组可化为$\left\{\begin{array}{l}{3x+4y=36①}\\{3x-2y=9②}\end{array}\right.$,
①-②得,6y=27,解得y=$\frac{9}{2}$,
把y=$\frac{9}{2}$代入②得,3x-9=9,解得x=6,
故此方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=\frac{9}{2}}\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案| A. | m=±1 | B. | m=-1 | C. | m=1 | D. | m的值不存在 |
| A. | 1,-1 | B. | 1,2 | C. | 1,-2 | D. | 1,1 |
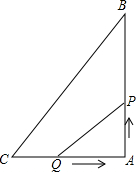 如图,在△ABC中,∠BAC=90°,AB=4cm,AC=3cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点A移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t秒.
如图,在△ABC中,∠BAC=90°,AB=4cm,AC=3cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点A移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t秒.

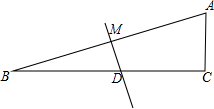 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长. 利用数轴解下列各题:
利用数轴解下列各题: