题目内容
2. 利用数轴解下列各题:
利用数轴解下列各题:(1)数轴上点A、点B分别是实数-3、2对应的点,则点A、点B间的距离为5.
(2)再选几个点试试,猜想:若点A、点B分别是实数a、b对应的点,则点A、点B间的距离为|b-a|.
(3)若数轴上点A对应的实数为a,且|a+2|+|a-1|=5,则点A对应的实数为-3或2.
分析 (1)根据数轴上两点间的距离是大数减小数,可得答案;
(2)根据数轴上两点间的距离是大数减小数,可得答案;
(3)分类讨论:a<-2,-2≤a<1,a≥1,根据绝对值的性质,可化简方程,根据解方程,可得答案.
解答 解:(1)数轴上点A、点B分别是实数-3、2对应的点,则点A、点B间的距离为2-(-3)=5;
(2)再选几个点试试,猜想:若点A、点B分别是实数a、b对应的点,则点A、点B间的距离为|b-a|;
(3)当a<-2时,原方程等价于-a-2+1-a=5,解得a=-3
当-2≤a<1时,原方程等价于a+2+1-a=5,方程无解;
当a≥1时,原方程等价于a+2+a-1=5,解得a=2,
综上所述a=-3或a=2,
故答案为:5,|b-a|,-3或2.
点评 本题考查了实数与数轴,数轴上两点间的距离是大数减小数,含绝对值的方程要分类讨论,以防遗漏.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
9.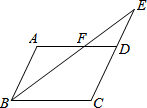 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,则图中的相似三角形对数共有( )
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,则图中的相似三角形对数共有( )
 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,则图中的相似三角形对数共有( )
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,则图中的相似三角形对数共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
7.下列说法正确的有( )个
①连接两点的线段的长叫两点之间的距离;
②直线比线段长;
③若AM=BM,则M为AB的中点;
④由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形.
①连接两点的线段的长叫两点之间的距离;
②直线比线段长;
③若AM=BM,则M为AB的中点;
④由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.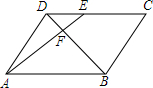 如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )
如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )
 如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )
如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )| A. | $\frac{4}{3}$ | B. | $\frac{16}{9}$ | C. | $\frac{3}{7}$ | D. | $\frac{7}{3}$ |
12.下列等式正确的是( )
| A. | (-1)0=-1 | B. | (-1)-1=1 | C. | 2x-2=$\frac{1}{{2{x^2}}}$ | D. | x-2y2=$\frac{y^2}{x^2}$ |
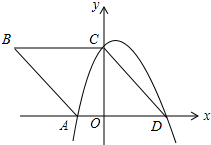 如图,在平面直角坐标系Oxy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=$\frac{4}{5}$.
如图,在平面直角坐标系Oxy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=$\frac{4}{5}$.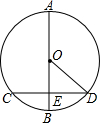 如图,在⊙O中,AB为直径,点B为$\widehat{CD}$的中点,直径AB交弦CD于E,CD=2$\sqrt{5}$,AE=5.
如图,在⊙O中,AB为直径,点B为$\widehat{CD}$的中点,直径AB交弦CD于E,CD=2$\sqrt{5}$,AE=5. 如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD,BC于E,F,延长BA交⊙A于G,判断弧EF和EG是否相等,并说明理由.
如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD,BC于E,F,延长BA交⊙A于G,判断弧EF和EG是否相等,并说明理由.