题目内容
9.若点C在线段AB的延长线上,线段AB=4cm,BC=6cm,点M、N分别是AC、BC的中点,线段MN=2cm.分析 根据线段的和差,可得AC的长,根据线段中点的性质,可得MC,NC的长,再根据线段的和差,可得答案.
解答 解:由线段的和差,得
AC=AB+BC=4+6=10cm.
由点M、N分别是AC、BC的中点,得
MC=$\frac{1}{2}$AC=$\frac{1}{2}$×10=5cm,NC=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3cm.
由线段的和差,得
MN=MC-NC=5-3=2cm.
故答案为:2cm.
点评 本题考查了两点间的距离,利用线段中点的性质得出MC,NC的长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 在数轴上表示a,b两个实数的点的位置如图所示,则化简|a+b|-|a-b|的结果为( )
在数轴上表示a,b两个实数的点的位置如图所示,则化简|a+b|-|a-b|的结果为( )
 在数轴上表示a,b两个实数的点的位置如图所示,则化简|a+b|-|a-b|的结果为( )
在数轴上表示a,b两个实数的点的位置如图所示,则化简|a+b|-|a-b|的结果为( )| A. | 2a | B. | 2b | C. | 2a-2b | D. | -2b |
1.计算12a5b6c4÷(-3a2b3c)÷(2a3b3c3),其结果是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
19. 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )
如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )
 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )
如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )| A. | ∠A+∠B=180° | B. | ∠D=∠DCG | C. | ∠B=∠DCG | D. | ∠B=∠AEF |
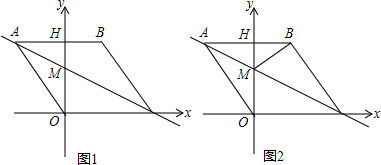
 如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD,BC于E,F,延长BA交⊙A于G,判断弧EF和EG是否相等,并说明理由.
如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD,BC于E,F,延长BA交⊙A于G,判断弧EF和EG是否相等,并说明理由.