题目内容
12．
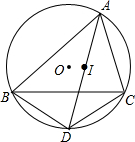如图，已知△ABC内接于⊙O，点I是△ABC的内心，AI的延长线交BC于点E，交⊙O于点D．求证：DB=DI=DC．
分析 连接BI，CI，要证明ID=BD=DC，只要求得∠BID=∠IBD，再根据角平分线的性质即可得到结论．
解答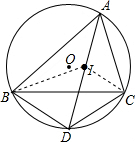 
证明：∵点I是△ABC的内心，
∴∠BAD=∠CAD，∠ABI=∠CBI，
∵∠CBD=∠CAD，
∴∠BAD=∠CBD，
∴∠BID=∠ABI+∠BAD，
∴∠ABI=∠CBI，∠BAD=∠CAD=∠CBD，
∵∠IBD=∠CBI+∠CBD，
∴∠BID=∠IBD，
∴ID=BD，
∵∠BAD=∠CAD，
∴$\widehat{BD}$=$\widehat{CD}$，
∴CD=BD，
∴DB=DC=DI．
点评 本题考查的是三角形的内切圆与内心，根据题意作出辅助线，构造出等腰三角形是解答此题的关键．
练习册系列答案
相关题目
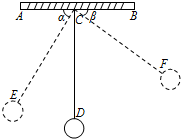如图，物理实验室有一单摆在左右摆动，摆动过程中选取了两个瞬时状态，从C处测得E、F两点的俯角分别为∠ACE=α，∠BCF=β，这时点F相对于点E升高了acm．求该摆绳CD的长度．（用含a、α、β的式子表示）
7．已知圆上均匀分布着2000个点，从中均等地选出A、B、C、D四个不同的点，则弦AB与CD相交的概率是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
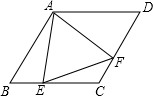如图，在菱形ABCD中，∠B=60°，若AB=2，点E是BC边上一动点，∠EAF=60°，AF交CD于点F