题目内容
17.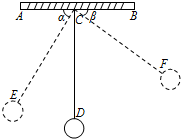 如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
分析 过点E、F作EG⊥CD,FH⊥CD,根据直角三角形的解法解答即可.
解答 解:分别过点E、F作EG⊥CD,FH⊥CD,垂足分别为G、H,
设摆绳CD的长度为xcm.则CE=CF=xcm.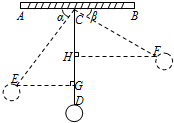 由题意知:HG=a,∠CEG=α,∠CFH=β.
由题意知:HG=a,∠CEG=α,∠CFH=β.
在Rt△CEG中,sin∠CEG=$\frac{CG}{CE}$,
∴CG=CE•sin∠CEG=x•sinα,
在Rt△CFH中,sin∠CFH=$\frac{CH}{CF}$,
∴CH=CF•sin∠CFH=x•sinβ.
∵HG=CG-CH,
∴x•sinα-x•sinβ=a,
解得x=$\frac{a}{sinα-sinβ}$.
答:摆绳CD的长度为$\frac{a}{sinα-sinβ}$cm.
点评 此题主要考查了解直角三角形中俯角问题的应用,根据锐角三角函数的关系得出CG与CH的长是解题关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
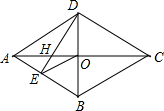 如图,四边形ABCD是菱形,对角线AC与BD相交于点O.DE⊥AB于点E.连接OE.
如图,四边形ABCD是菱形,对角线AC与BD相交于点O.DE⊥AB于点E.连接OE.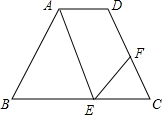 如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°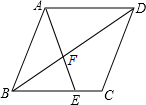 如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.
如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.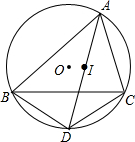 如图,已知△ABC内接于⊙O,点I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D.
如图,已知△ABC内接于⊙O,点I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D. 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.